题目内容
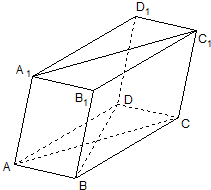
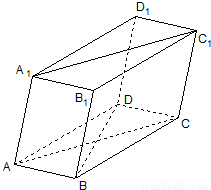
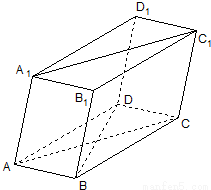
如图棱柱ABCD-A1B1C1D1的底面是菱形,平面AA1C1C⊥平面ABCD;(Ⅰ)求证:BD⊥AA1;
(Ⅱ)设AB=a,∠BAC=30°,四边形AA1C1C的面积为3a2,求棱柱ABCD-A1B1C1D1的体积、
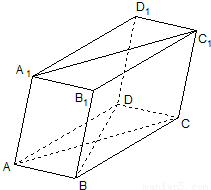
【答案】分析:(I)由已知中棱柱ABCD-A1B1C1D1的底面是菱形,平面AA1C1C⊥平面ABCD,我们根据菱形的性质及面面垂直的性质定理,易得BD⊥平面AA1C1C,再由线面垂直的性质,即可得到BD⊥AA1;
(Ⅱ)由已知中AB=a,∠BAC=30°,四边形AA1C1C的面积为3a2,我们可计算出棱柱底面ABCD的面积及高AA1的长度,然后代入棱柱体积公式,即可得到答案.
解答:证明:(Ⅰ)∵棱柱ABCD-A1B1C1D1的底面是菱形,
∴AC⊥BD,
又∵平面AA1C1C⊥平面ABCD
∴BD⊥平面AA1C1C
又由AA1?平面AA1C1C
∴BD⊥AA1;
(Ⅱ)∵AB=a,∠BAC=30°,
则AC= ,BD=a
,BD=a
∴SABCD=2× AB•AD•sin∠A=
AB•AD•sin∠A=
又四边形AA1C1C的面积为3a2,
∴AA1= ,
,
∴V=AA1•SABCD=
点评:本题考查的知识点是直线与平面垂直的性质,棱柱的体积,熟练掌握空间直线与直线、直线与平面、平面与平面之间垂直关系的相互转化是解答本题的关键.
(Ⅱ)由已知中AB=a,∠BAC=30°,四边形AA1C1C的面积为3a2,我们可计算出棱柱底面ABCD的面积及高AA1的长度,然后代入棱柱体积公式,即可得到答案.
解答:证明:(Ⅰ)∵棱柱ABCD-A1B1C1D1的底面是菱形,
∴AC⊥BD,
又∵平面AA1C1C⊥平面ABCD
∴BD⊥平面AA1C1C
又由AA1?平面AA1C1C
∴BD⊥AA1;
(Ⅱ)∵AB=a,∠BAC=30°,
则AC=
 ,BD=a
,BD=a∴SABCD=2×
 AB•AD•sin∠A=
AB•AD•sin∠A=
又四边形AA1C1C的面积为3a2,
∴AA1=
 ,
,∴V=AA1•SABCD=

点评:本题考查的知识点是直线与平面垂直的性质,棱柱的体积,熟练掌握空间直线与直线、直线与平面、平面与平面之间垂直关系的相互转化是解答本题的关键.

练习册系列答案
相关题目