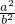题目内容
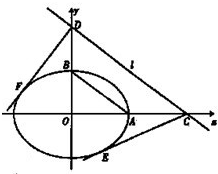 如图,已知A,B分别为椭圆
如图,已知A,B分别为椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、±
| ||
B、±
| ||
C、±
| ||
D、±
|
分析:不妨令CD与该椭圆相切,切点为H,利用对称性,将复杂问题简单好,即可解决问题.
解答: 解:依题意,不妨令CD与该椭圆相切,切点为H,则切点F与H关于y轴对称,切点E与H关于x轴对称,如图,
解:依题意,不妨令CD与该椭圆相切,切点为H,则切点F与H关于y轴对称,切点E与H关于x轴对称,如图,
∵kAB=-
,直线 l∥AB,
∴kCD=-
,
∴kDF=
(切点F在第二象限),或kDF=-
(切点F在第一象限);
同理可得,kCE=
(切点E在第四象限),或kCE=-
(切点E在第一象限);
∴CE与DF的斜率之积kCE•kDF=±
.
故选:C.
 解:依题意,不妨令CD与该椭圆相切,切点为H,则切点F与H关于y轴对称,切点E与H关于x轴对称,如图,
解:依题意,不妨令CD与该椭圆相切,切点为H,则切点F与H关于y轴对称,切点E与H关于x轴对称,如图,∵kAB=-
| b |
| a |
∴kCD=-
| b |
| a |
∴kDF=
| b |
| a |
| b |
| a |
同理可得,kCE=
| b |
| a |
| b |
| a |
∴CE与DF的斜率之积kCE•kDF=±
| b2 |
| a2 |
故选:C.
点评:本题考查椭圆的简单性质,将CD特殊化处理(与椭圆相切)是关键,考查化归思想,分类讨论思想,数形结合思想的综合运用,考查分析问题、解决问题的能力,属于难题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N.
如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N. 如图,已知A、B为椭圆
如图,已知A、B为椭圆 如图,已知A,B分别为椭圆
如图,已知A,B分别为椭圆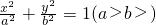 的右顶点和上顶点,直线 l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE•kDF等于
的右顶点和上顶点,直线 l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE•kDF等于