题目内容
已知O是△ABC的外心，AB=2a，AC=
，∠BAC=120°，若
=x
+y
，则x+y的最小值是
| 2 |
| a |
| AO |
| AB |
| AC |
2
2
．分析：建立直角坐标系，求出三角形各顶点的坐标，因为O为△ABC的外心，把AB的中垂线 m方程和AC的中垂线 n的方程，联立方程组，求出O的坐标，利用已知向量间的关系，待定系数法求x和y的值，最后利用基本不等式求最小值即可．
解答：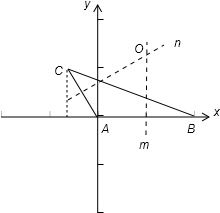
解：如图：以A为原点，以AB所在的直线为x轴，建立直角系：
则A（0，0），B （2a，0），C（-
，
），
∵O为△ABC的外心，
∴O在AB的中垂线 m：x=a上，又在AC的中垂线 n 上，
AC的中点（-
，
），AC的斜率为tan120°=-
，
∴中垂线n的方程为 y-
=
（x+
）．
把直线 m和n 的方程联立方程组
，
解得△ABC的外心O（a，
a+
），
由条件
=x
+y
，得（a，
a+
）
=x（2a，0）+y（-
，
）=（2ax-
，
），
∴
，解得x=
+
，y=
+
，
∴x+y=
+
+
+
=
+
（
+a2）≥
+
×2=2．
当且仅当a=1时取等号．
故答案为：2．
解：如图：以A为原点，以AB所在的直线为x轴，建立直角系：则A（0，0），B （2a，0），C（-
| 1 |
| a |
| ||
| a |
∵O为△ABC的外心，
∴O在AB的中垂线 m：x=a上，又在AC的中垂线 n 上，
AC的中点（-
| 1 |
| 2a |
| ||
| 2a |
| 3 |
∴中垂线n的方程为 y-
| ||
| 2a |
| ||
| 3 |
| 1 |
| 2a |
把直线 m和n 的方程联立方程组
|
解得△ABC的外心O（a，
| ||
| 3 |
2
| ||
| 3a |
由条件
| AO |
| AB |
| AC |
| ||
| 3 |
2
| ||
| 3a |
=x（2a，0）+y（-
| 1 |
| a |
| ||
| a |
| y |
| a |
| ||
| a |
∴
|
| 2 |
| 3 |
| 1 |
| 3a2 |
| a2 |
| 3 |
| 2 |
| 3 |
∴x+y=
| 2 |
| 3 |
| 1 |
| 3a2 |
| a2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| a2 |
| 4 |
| 3 |
| 1 |
| 3 |
当且仅当a=1时取等号．
故答案为：2．
点评：本题考查求两条直线的交点坐标的方法，三角形外心的性质，向量的坐标表示及向量相等的条件，待定系数法求参数值．属中档题．
练习册系列答案
相关题目