Question

已知非零向量e₁、e₂不共线，如果=e₁+e₂,=2e₁+8e₂,=3e₁-3e₂,

求证：A、B、C、D共面.

Answer 1

证明：令λ(e₁+e₂)+μ(2e₁+8e₂)+v(3e₁-3e₂)=0,

则(λ+2μ+3v)e₁+(λ+8μ-3v)e₂=0.

∵e₁、e₂不共线,∴易知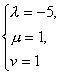是其中一组解.

则,

∴A、B、C、D共面.

启示：用空间向量基本定理，结合向量的运算法则，把一个向量用其他向量表示出来.按照这个方法，只要存在三个非零实数，使其向量之和为零向量，则这三个向量就共面，从而证明四点共面.