题目内容

f（x）是y=2-x2和y=x两个函数中较小者，则f（x）的最大值是
1
1
．
分析：先根据题目条件得到函数：f（x）=
2-x2，x＞1或x＜-2
x     ， -2≤x≤1
，然后按照每一段求出最大值，得出结论．
解答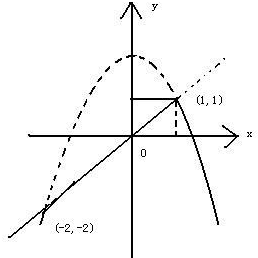：解：根据题意有：2-x2=x，
∴x2+x-2=0，
即（x+2）（x-1）=0，
解得x=1，x=-2．
∴f（x）=
2-x2，x＞1或x＜-2
x     ， -2≤x≤1
，
当x＞1或x＜-2时，f（x）≤1．
当-2≤x≤1时，f（x）≤1．
综上：f（x）的最大值是1．
故答案为：1．
点评：本题考查二次函数的性质，要注意构造函数，以及考查分段函数的最值，属中档题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
已知函数f（x）=（1+x）t-1的定义域为（-1，+∞），其中实数t满足t≠0且t≠1．直线l：y=g（x）是f（x）的图象在x=0处的切线．
（1）求l的方程：y=g（x）；
（2）若f（x）≥g（x）恒成立，试确定t的取值范围；
（3）若a1，a2∈（0，1），求证：
a
a1
1
+
a
a2
2
≥
a
a2
1
+
a
a1
2
．
注：当α为实数时，有求导公式（xα）′=αxα-1．
（2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2-n）与2-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．
下列命题中
①对于每一个实数x，f（x）是y=2-x2和y=x这两个函数中的较小者，则f（x）的最大值是1．
②已知x1是方程x+lgx=3的根，x2是方程x+10x=3的根，则x1+x2=3．
③函数f（x）=ax2+bx+3a+b是偶函数，其定义域为[a-1，2a]，则f（x）的图象是以（0，1）为顶点，开口向下的抛物线．
④若集合P={x|x=3m+1，m∈N+}，Q={x|x=5n+2，n∈N+}，则P∩Q={x|x=15m-8，m∈N+}
⑤若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中正确的命题的序号是
①②④⑤
①②④⑤
．
下列命题中
①对于每一个实数x，f（x）是y=2-x2和y=x这两个函数中的较小者，则f（x）的最大值是1．
②已知x1是方程x+lgx=3的根，x2是方程x+10x=3的根，则x1+x2=3．
③函数f（x）=ax2+bx+3a+b是偶函数，其定义域为[a-1，2a]，则f（x）的图象是以（0，1）为顶点，开口向下的抛物线．
④若集合P={x|x=3m+1，m∈N+}，Q={x|x=5n+2，n∈N+}，则P∩Q={x|x=15m-8，m∈N+}
⑤若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中正确的命题的序号是    ．
对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2-n）与2-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网