题目内容
已知函数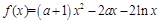 .
.
(1)求证: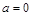 时,
时,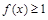 恒成立;
恒成立;
(2)当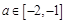 时,求
时,求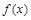 的单调区间.
的单调区间.
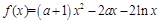 .
.(1)求证:
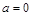 时,
时,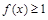 恒成立;
恒成立;(2)当
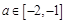 时,求
时,求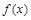 的单调区间.
的单调区间.(1)详见试题解析;(2)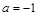 时,
时,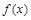 的单调递增区间为
的单调递增区间为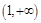 ,单调递减区间为
,单调递减区间为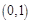 ;
;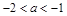 时,
时,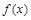 的单调递增区间为
的单调递增区间为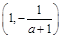 ,单调递减区间为
,单调递减区间为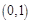 和
和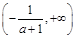 ;
;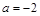 时,
时,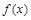 的单调递减区间为
的单调递减区间为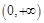 ,无单调增区间.
,无单调增区间.
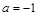 时,
时,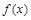 的单调递增区间为
的单调递增区间为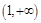 ,单调递减区间为
,单调递减区间为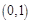 ;
;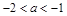 时,
时,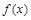 的单调递增区间为
的单调递增区间为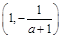 ,单调递减区间为
,单调递减区间为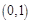 和
和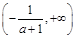 ;
;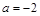 时,
时,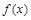 的单调递减区间为
的单调递减区间为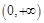 ,无单调增区间.
,无单调增区间.试题分析:(1)当
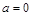 时,
时,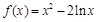 ,根据求函数极值的一般步骤,先求函数
,根据求函数极值的一般步骤,先求函数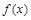 的定义域,再求导数,解
的定义域,再求导数,解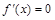 的方程,得可能的极值点,进一步得函数
的方程,得可能的极值点,进一步得函数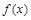 的单调性,最后得
的单调性,最后得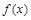 的最小值,从而证得
的最小值,从而证得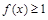 恒成立;(2)当
恒成立;(2)当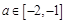 时,先求
时,先求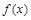 的导数:
的导数: ,根据
,根据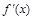 表达式的结构特征,分子为
表达式的结构特征,分子为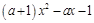 ,故只需分
,故只需分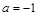 ,
,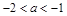 ,
,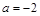 几种情况,分别求函数
几种情况,分别求函数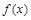 的单调区间.
的单调区间.试题解析:(1)当
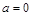 时,
时,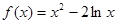 ,
,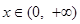 ,
,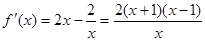 ,令
,令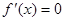 ,解得:
,解得: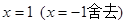 .当
.当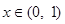 时,
时,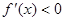 ,
,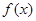 在
在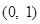 上单调递减; 当
上单调递减; 当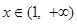 时,
时, ,
,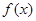 在
在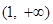 上单调递增,∴
上单调递增,∴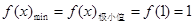 .
. 所以,
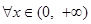 ,
, 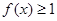 . 5分
. 5分(2)
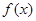 的定义域为
的定义域为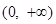 ,
,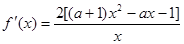 .
. ①当
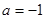 时,
时,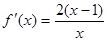 ,此时
,此时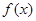 在区间
在区间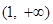 上单调递增,在
上单调递增,在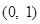 上单调递减;
上单调递减;②当
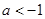 时,
时,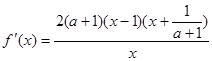 .令
.令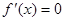 ,解得:
,解得: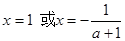 .
.ⅰ)当
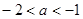 时,
时,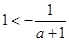 ,令
,令 ,解得:
,解得: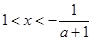 .令
.令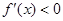 ,解得:
,解得: 或
或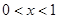 ,此时
,此时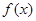 在区间
在区间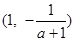 上单调递增,在
上单调递增,在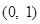 和
和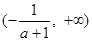 上单调递减.
上单调递减.ⅱ)当
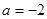 时,
时,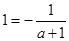 ,此时
,此时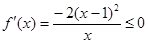 ,
,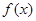 在区间
在区间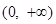 上单调递减.
上单调递减.综上,
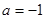 时,
时,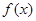 的单调递增区间为
的单调递增区间为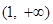 ,单调递减区间为
,单调递减区间为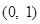 ;
;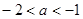 时,
时,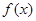 的单调递增区间为
的单调递增区间为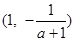 ,单调递减区间为
,单调递减区间为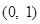 和
和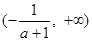 ;
;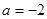 时,
时,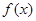 的单调递减区间为
的单调递减区间为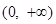 ,无单调增区间. 13分
,无单调增区间. 13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
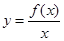 在
在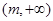 上为增函数(
上为增函数( 为常数),则称
为常数),则称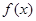 为区间
为区间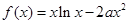 是
是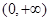 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数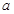 的取值范围;
的取值范围;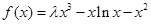 (
(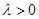 ,
,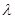 为常数),且
为常数),且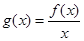 有唯一的零点,求
有唯一的零点,求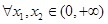 ,
,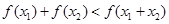
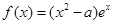 .
.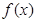 在
在 上不是单调函数,求实数
上不是单调函数,求实数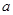 的取值范围;
的取值范围;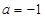 时,讨论函数
时,讨论函数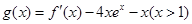 的零点个数.
的零点个数.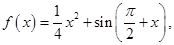
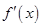 为
为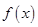 的导函数,则
的导函数,则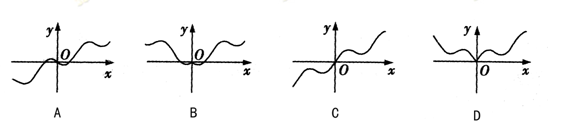
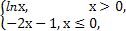 D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为 .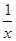 -1.
-1.