题目内容
当m取哪些值时,直线y=x+m与椭圆| x2 |
| 16 |
| y2 |
| 9 |
分析:直线与椭圆的交点适合下面方程组:
,①代入②得
+
=1,其判别式为△=576(25-m2).由此可知直线与椭圆有一个交点的充要条件是m=±5,这时直线与椭圆相切.直线与椭圆有两个交点的充要条件是:-m2+25>0即|m|<5,这时直线与椭圆相割.直线与椭圆没有交点的充要条件是:-m2+25<0,即|m|>5.
|
| x2 |
| 16 |
| (x+m)2 |
| 9 |
解答:解:直线与椭圆的交点适合下面方程组:
将①代入②得
+
=1,
整理可得25x2+32mx+(16m2-144)=0,
其判别式为△=(32m)2-4•25•(16m2-144)=576(25-m2)
直线与椭圆有一个交点的充要条件是m=±5,
这时直线与椭圆相切.
直线与椭圆有两个交点的充要条件是:-m2+25>0即|m|<5,
这时直线与椭圆相割.
直线与椭圆没有交点的充要条件是:-m2+25<0,即|m|>5.
|
将①代入②得
| x2 |
| 16 |
| (x+m)2 |
| 9 |
整理可得25x2+32mx+(16m2-144)=0,
其判别式为△=(32m)2-4•25•(16m2-144)=576(25-m2)
直线与椭圆有一个交点的充要条件是m=±5,
这时直线与椭圆相切.
直线与椭圆有两个交点的充要条件是:-m2+25>0即|m|<5,
这时直线与椭圆相割.
直线与椭圆没有交点的充要条件是:-m2+25<0,即|m|>5.
点评:本题考查直线和圆锥曲线的位置关系,解题时要注意公式的灵活运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
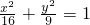 有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.
有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象. 有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.
有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.