题目内容
已知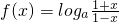 (a>0,且a≠1),
(a>0,且a≠1),
(1)判断奇偶性,并证明;
(2)求使f(x)<0的x的取值范围.
解:(1)f(x)为奇函数.
证明如下:
由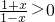 得函数的定义域为(-1,1),
得函数的定义域为(-1,1),
又f(-x)= =
= =-
=-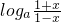 =-f(x),
=-f(x),
所以,f(x)为奇函数.
(2)由题意:当0<a<1时,有 解得0<x<1;
解得0<x<1;
当a>1时,有 解得-1<x<0;
解得-1<x<0;
综上,当0<a<1时,0<x<1; 当a>1时,-1<x<0.
分析:(1)先求出定义域,然后利用奇偶性的定义即可判断;
(2)分0<a<1,a>1两种情况讨论,当0<a<1时,有 ,当a>1时,有
,当a>1时,有 ,分别解出即可;
,分别解出即可;
点评:本题考查函数奇偶性的判断及对数不等式的求解,考查分类讨论思想.
证明如下:
由
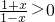 得函数的定义域为(-1,1),
得函数的定义域为(-1,1),又f(-x)=
 =
= =-
=-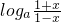 =-f(x),
=-f(x),所以,f(x)为奇函数.
(2)由题意:当0<a<1时,有
 解得0<x<1;
解得0<x<1;当a>1时,有
 解得-1<x<0;
解得-1<x<0;综上,当0<a<1时,0<x<1; 当a>1时,-1<x<0.
分析:(1)先求出定义域,然后利用奇偶性的定义即可判断;
(2)分0<a<1,a>1两种情况讨论,当0<a<1时,有
 ,当a>1时,有
,当a>1时,有 ,分别解出即可;
,分别解出即可;点评:本题考查函数奇偶性的判断及对数不等式的求解,考查分类讨论思想.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目