题目内容
设全集 ,集合
,集合 ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
A
解析试题分析:因为 ,
,
所以 =
= =
= ,故选A。
,故选A。
考点:本题主要考查集合的运算,一元二次不等式解法。
点评:基础题,关键是理解集合M,N中元素的特征。

练习册系列答案
相关题目
设集合A= ,B=
,B= ,则
,则 ( )
( )
A. | B. | C.(3,4) | D.(1,2) |
若集合 ,
, ,那么
,那么 =( )
=( )
A. | B. | C. | D.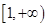 |
设集合M={x∣x<2},集合N={x∣0<x<1},则下列关系中正确的是( )
| A. M∪N=R | B. M∪СRN=R | C. N∪СRM=R | D. M∩N=M |
若全集 ,则集合
,则集合 的真子集共有( )
的真子集共有( )
A. 个 个 | B.5个 | C.7个 | D. 个 个 |
设集合 ,则
,则
A. | B. |
| C.2 | D.-2 |
已知全集 ,集合
,集合 ,则图中阴影部分表示的集合为( )
,则图中阴影部分表示的集合为( )
A. | B. | C. | D. |
设 ,则 ( )
,则 ( )
A. | B. | C. | D. |
已知集合 ,
, ,则
,则 ( )
( )
A. | B. |
C. | D. |