题目内容
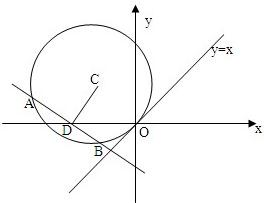
在直角坐标系xOy中,以坐标原点O为圆心的圆与直线:x-
y=4相切.
(1)求圆O的方程;
(2)若圆O上有两点M、N关于直线x+2y=0对称,且|MN|=2
,求直线MN的方程.
| 3 |
(1)求圆O的方程;
(2)若圆O上有两点M、N关于直线x+2y=0对称,且|MN|=2
| 3 |
(本题满分14分)
(1)依题设,圆O的半径r等于原点O到直线x-
y=4的距离,
即r=
=2.…(3分)
得圆O的方程为x2+y2=4.…(6分)
(2)由题意,可设直线MN的方程为2x-y+m=0.…(8分)
则圆心O到直线MN的距离d=
.…(10分)
由垂径分弦定理得:
+(
)2=22,即m=±
.…(12分)
所以直线MN的方程为:2x-y+
=0或2x-y-
=0.…(14分)
(1)依题设,圆O的半径r等于原点O到直线x-
| 3 |
即r=
| 4 | ||
|
得圆O的方程为x2+y2=4.…(6分)
(2)由题意,可设直线MN的方程为2x-y+m=0.…(8分)
则圆心O到直线MN的距离d=
| |m| | ||
|
由垂径分弦定理得:
| m2 |
| 5 |
| 3 |
| 5 |
所以直线MN的方程为:2x-y+
| 5 |
| 5 |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 、
、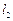 是通过某城市开发区中心
是通过某城市开发区中心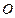 的两条南北和东西走向的街道,连接
的两条南北和东西走向的街道,连接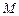 、
、 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在 上的一段圆弧.若点
上的一段圆弧.若点 在点
在点 ,点
,点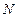 到
到 和
和 .
. ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).