题目内容
已知函数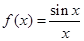 .
.
(Ⅰ)下列三种说法:①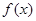 是偶函数;②
是偶函数;②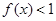 ;③当
;③当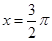 时,
时,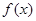 取得极小值. 其中正确的说法有____________;(写出所有正确说法的序号)
取得极小值. 其中正确的说法有____________;(写出所有正确说法的序号)
(Ⅱ)满足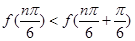 的正整数
的正整数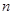 的最小值为________
的最小值为________
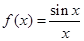 .
.(Ⅰ)下列三种说法:①
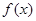 是偶函数;②
是偶函数;②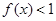 ;③当
;③当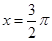 时,
时,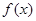 取得极小值. 其中正确的说法有____________;(写出所有正确说法的序号)
取得极小值. 其中正确的说法有____________;(写出所有正确说法的序号)(Ⅱ)满足
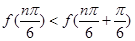 的正整数
的正整数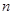 的最小值为________
的最小值为________(Ⅰ)①② ;(Ⅱ)

(Ⅰ) 的定义域为
的定义域为 ,关于原点对称,且
,关于原点对称,且 ,所以
,所以 是偶函数,命题①正确;
是偶函数,命题①正确;

对于②,针对函数 的性质,只须考虑当
的性质,只须考虑当 时的函数值即可,如图,在单位圆中,有
时的函数值即可,如图,在单位圆中,有 ,连接
,连接 ,则
,则 。设
。设 的长为l,则
的长为l,则 ,所以
,所以 ,即
,即 ,故
,故 ,所以
,所以 ,命题②正确;
,命题②正确;
 ,令
,令 可得
可得 ,即
,即 ,此时
,此时 取到极值。当
取到极值。当 时,
时, ,所以
,所以 不是
不是 的极值点,命题③不正确。
的极值点,命题③不正确。
综上可得,正确的命题为①②
(Ⅱ)当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 ;
;
当 时,
时, ,此时
,此时 。
。
所以满足 的正整数
的正整数 的最小值是9
的最小值是9
 的定义域为
的定义域为 ,关于原点对称,且
,关于原点对称,且 ,所以
,所以 是偶函数,命题①正确;
是偶函数,命题①正确;
对于②,针对函数
 的性质,只须考虑当
的性质,只须考虑当 时的函数值即可,如图,在单位圆中,有
时的函数值即可,如图,在单位圆中,有 ,连接
,连接 ,则
,则 。设
。设 的长为l,则
的长为l,则 ,所以
,所以 ,即
,即 ,故
,故 ,所以
,所以 ,命题②正确;
,命题②正确; ,令
,令 可得
可得 ,即
,即 ,此时
,此时 取到极值。当
取到极值。当 时,
时, ,所以
,所以 不是
不是 的极值点,命题③不正确。
的极值点,命题③不正确。综上可得,正确的命题为①②
(Ⅱ)当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 ;
;当
 时,
时, ,此时
,此时 。
。所以满足
 的正整数
的正整数 的最小值是9
的最小值是9
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
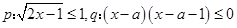 .若
.若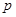 是
是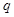 的充分不必要条件,则实数
的充分不必要条件,则实数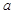 的取值范围是( )
的取值范围是( )



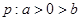 ,命题
,命题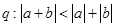 ,则命题
,则命题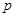 是
是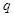 的
的 



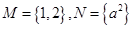 ,则“
,则“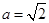 ”是“
”是“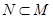 ”的( )
”的( )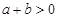 的一个充分不必要条件是 。
的一个充分不必要条件是 。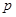 :
: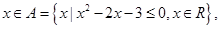
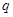 :
: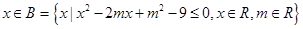
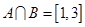 ,求实数
,求实数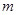 的值;
的值;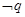 的充分条件,求实数
的充分条件,求实数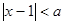 成立的一个充分条件为
成立的一个充分条件为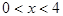 ,则实数a的取值范围为 .
,则实数a的取值范围为 .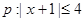 ,条件
,条件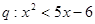 ,则
,则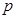 是
是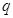 的( )
的( )