题目内容
求函数y=sin4x+2
sinxcosx-cos4x的最小正周期、最小值和单调递增区间．
| 3 |
y=sin4x+2
sinxcosx-cos4x
=sin4x-cos4x+2
sinxcosx
=（sin2x+cos2x）（sin2x-cos2x）+2
sinxcosx
=-cos2x+
sin2x
=2（sin2xcos
-cos2xsin
）
=2sin（2x-
）
∴T=
=π，ymin=-2，
又∵-
+2kπ≤2x-
≤
+2kπ，
∴-
+2kπ≤2x≤
+2kπ，即-
+kπ≤x≤
+kπ，
所以y=2sin（2x-
）的单调增区间是[-
+kπ，
+kπ]
| 3 |
=sin4x-cos4x+2
| 3 |
=（sin2x+cos2x）（sin2x-cos2x）+2
| 3 |
=-cos2x+
| 3 |
=2（sin2xcos
| π |
| 6 |
| π |
| 6 |
=2sin（2x-
| π |
| 6 |
∴T=
| 2π |
| 2 |
又∵-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
所以y=2sin（2x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
练习册系列答案
相关题目
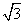sinxcosx-cos4x的最小正周期和最小值；并写出该函数在[0，π]上的单调递增区间。
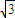sinxcosx-cos4x的最小正周期和最小值；并写出该函数在[0，π]上的单调递增区间．
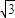sinxcosx-cos4x的最小正周期和最小值；并写出该函数在[0，π]上的单调递增区间．