题目内容
16.某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(2≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)万件.(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).
分析 (1)通过利润=销售量×售价,代入计算即可;
(2)通过配方,考查对称轴的位置即可.
解答 解:(1)L(x)=(x-3-a)(12-x)(9≤x≤11);
(2)$L(x)=(x-3-a)(12-x)=-{(x-\frac{15+a}{2})^2}+{(\frac{9-a}{2})^2}$,
∵2≤a≤5,
∴当$\frac{15+a}{2}$<9即2≤a<3时,Q(a)=L(9)=18-3a,
当$\frac{15+a}{2}$≥9即3≤a≤5时,Q(a)=L($\frac{15+a}{2}$)=$(\frac{9-a}{2})^{2}$,
∴Q(a)=$\left\{\begin{array}{l}{(\frac{9-a}{2})^{2},}&{3≤a≤5}\\{18-3a,}&{2≤a<3}\end{array}\right.$.
点评 本题考查函数模型的选择与应用,分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
18.已知,a,b,c(a>b>c)是△ABC的角A,B,C的对边,若4sin2(B+C)-3=0,则$\frac{asin(\frac{π}{6}-C)}{b-c}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
7.下列各组中的两个函数是相同函数的为( )
| A. | f(x)=$\frac{(x+3)(x-5)}{x+3}$,g(x)=x-5 | B. | f(x)=x,g(x)=$\sqrt{x^2}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{x^3}$ | D. | f(x)=$\sqrt{x+1}\sqrt{x-1}$,g(x)=$\sqrt{(x+1)(x-1)}$ |
4.平移函数y=|sinx|的图象得到函数y=|cosx|的图象,以下平移方法错误的是( )
| A. | 向左或向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左或向右平移$\frac{3π}{2}$个单位 |
1.已知$\overrightarrow a=(-3,2),\overrightarrow b=(-1,-1)$,向量λ$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-2\overrightarrow b$垂直,则实数λ的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{11}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
8.有下列四个命题,其中真命题有:
①“若x+y=0,则x、y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1,则x2+2x+q=0有实根”的逆命题
④“不等边三角形的三个内角相等”的逆否命题,其中真命题的序号为( )
①“若x+y=0,则x、y互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若q≤1,则x2+2x+q=0有实根”的逆命题
④“不等边三角形的三个内角相等”的逆否命题,其中真命题的序号为( )
| A. | ①③ | B. | ②③ | C. | ①② | D. | ③④ |
5.函数y=sin(ωx+φ)的部分图象如图,则f($\frac{π}{2}$)=( )


| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
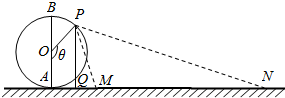 如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).
如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).