题目内容
奇函数f(x)的定义域为R,若f(x+2)为偶函数,则f(1)=1,则f(8)+f(9)= ( )
| A.-2 | B.-1 | C.0 | D.1 |
D
解析试题分析:因为函数f(x)是奇函数,所以f(-x)=-f(x),又因为f(x+2)是偶函数,所以f(-x+2)= f(x+2),所以f(8)=f(6+2)=f(-6+2)=f(-4)=-f(4),而f(4)=f(2+2)=f(-2+2)=f(0)=0,f(8)=0,同理f(9)=f(7+2)=f(-7+2)=f(-5)=-f(5),而f(5)=(3+2)=f(-3+2)=f(-1)=-f(1)=-1,f(9)=1.所以f(8) +f(9)=1,故选D.
【考点】函数的奇偶性和周期性,

练习册系列答案
相关题目
函数 的图象( ).
的图象( ).
| A.关于原点对称 | B.关于直线y=x对称 |
| C.关于x轴对称 | D.关于y轴对称 |
已知函数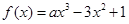 ,若
,若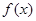 存在唯一的零点
存在唯一的零点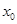 ,且
,且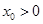 ,则
,则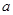 的取值范围是
的取值范围是
A.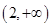 | B.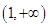 | C.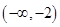 | D.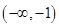 |
已知偶函数 在区间
在区间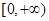 单调递增,则满足
单调递增,则满足 的x取值范围是( )
的x取值范围是( )
A. | B. | C. | D. |
已知函数 ,
, ,若
,若 ,则
,则 ( )
( )
| A.1 | B.2 | C.3 | D.-1 |
已知函数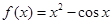 ,则
,则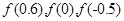 的大小关系是( )
的大小关系是( )
A.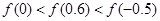 |
B.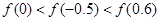 |
C.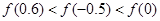 |
D.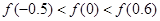 |
若函数f(x)、g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
 的图像大致是( )
的图像大致是( )




