Question

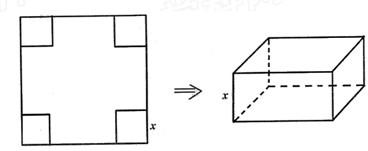
从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形，再将四边向上折起，做成一个无盖长方体铁盒，要求长方体的高度与底面边长的比值不超过常数t(t＞0).试问当x取何值时，容积V有最大值.

Answer 1

解：V=x(2a-2x)²=4(a-x)²·x.

∵≤t,

∴0＜x≤,

∴函数V=V（x）=4x(a-x)²的定义域为（0，,

显然＜a,

∴V′=4(x-a)(3x-a),由V′＞0,得0＜x＜或x＞a,此时V(x)为增函数；

由V′＜0,得＜x＜a,此时V（x）为减函数.

①当≤,即t≥时，在x=时，V有最大值a³;

②当＜,即0＜t＜时，在x=时，V有最大值.