题目内容
在△ABC中,∠C=60°,则cosAcosB的取值范围是
- A.
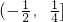
- B.
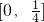
- C.
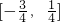
- D.以上都不对
A
分析:先根据积化和差公式进行化简,再由C=60°确定A+B的值并代入从而可确定cosAcosB=- +
+ cos(A-B),再由A-B的范围可确定cos(A-B)的范围进而确定最后答案.
cos(A-B),再由A-B的范围可确定cos(A-B)的范围进而确定最后答案.
解答:∵cosAcosB= [cos(A+B)+cos(A-B)]
[cos(A+B)+cos(A-B)]
= cos120°+
cos120°+ cos(A-B)
cos(A-B)
=- +
+ cos(A-B)
cos(A-B)
当A-B=0时,cos(A-B)有最大值1
当A-B=120°时,cos(A-B)有最小值- ,但不能取到
,但不能取到
- +
+ ×1=
×1=
- +(
+( )*(-
)*(- )=-
)=-
即cosAcosB属于(- ,
, ]
]
故选A.
点评:本题主要考查积化和差公式的应用和余弦函数的单调性.考查基础知识的综合应用.三角函数是高考的一个重要考点要强化复习.
分析:先根据积化和差公式进行化简,再由C=60°确定A+B的值并代入从而可确定cosAcosB=-
 +
+ cos(A-B),再由A-B的范围可确定cos(A-B)的范围进而确定最后答案.
cos(A-B),再由A-B的范围可确定cos(A-B)的范围进而确定最后答案.解答:∵cosAcosB=
 [cos(A+B)+cos(A-B)]
[cos(A+B)+cos(A-B)]=
 cos120°+
cos120°+ cos(A-B)
cos(A-B)=-
 +
+ cos(A-B)
cos(A-B)当A-B=0时,cos(A-B)有最大值1
当A-B=120°时,cos(A-B)有最小值-
 ,但不能取到
,但不能取到-
 +
+ ×1=
×1=
-
 +(
+( )*(-
)*(- )=-
)=-
即cosAcosB属于(-
 ,
, ]
]故选A.
点评:本题主要考查积化和差公式的应用和余弦函数的单调性.考查基础知识的综合应用.三角函数是高考的一个重要考点要强化复习.

练习册系列答案
相关题目
