Question

【题目】已知二次函数f（x）=ax2+bx+c．
（1）若a=c＞0，f（1）=1，对任意x∈|[﹣2，2]，f（x）的最大值与最小值之和为g（a），求g（a）的表达式；
（2）若a，b，c为正整数，函数f（x）在（﹣ ， ）上有两个不同零点，求a+b+c的最小值．

Answer 1

【答案】
（1）解：a=c＞0，f（1）=1，则a+b+a=1，b=1﹣2a，

∴f（x））=ax2+（1﹣2a）x+a=a + ，

当1﹣ ≤﹣2，即0＜a≤ 时，g（a）=f（﹣2）+f（2）=10a；

当﹣2＜1﹣ ≤0，即 ＜a≤ 时，g（a）=f（1﹣ ）+f（2）=a﹣ +3，

当a＞ 时，g（a）=f（1﹣ ）+f（﹣2）=9a﹣ ﹣1，

综上所述，g（a）=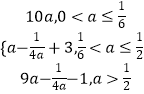

（2）解：函数f（x）在（﹣ ， ）上有两个不同零点x1，x2，则x1+x2=﹣ ＜0， ＞x1x2= ＞0

∴a＞16c，

由根的分布可知f（﹣ ）= a﹣ b+c＞0，即a+16c＞4b，

∵a，b，c为正整数，∴a+16c≥4b+1

f（0）=c＞0，△＞0，b ，

∴a+16c＞8 +1，可得（ ）2＞1，

∵a＞16c，∴ ＞1，

∴ ，∴a＞25，

∴a≥26，

∴b ≥ ，∴b≥11，c≥1．

f（x）=26x2+11x+1，经检验符合题意，故a+b+c的最小值为38

【解析】（1）配方，分类讨论，求g（a）的表达式；（2）若a，b，c为正整数，函数f（x）在（﹣ ， ）上有两个不同零点，确定a，b，c的范围，即可求a+b+c的最小值．