题目内容
(2012•通州区一模)已知函数f(x)=lnx-a2x2+ax(a∈R).
(1)当a=1时,求函数f(x)最大值;
(2)若函数f(x)在区间(1,+∞)上是减函数,求实数a的取值范围.
(1)当a=1时,求函数f(x)最大值;
(2)若函数f(x)在区间(1,+∞)上是减函数,求实数a的取值范围.
分析:(1)把a=1代入函数,利用导数判断出函数的单调性,进而可求出函数f(x)最大值;
(2)对参数a进行讨论,然后利用导数f′(x)≤0(注意函数的定义域)来解答,方法一是先解得单调减区间A,再与已知条件中的减区间(1,+∞)比较,即只需要(1,+∞)⊆A即可解答参数的取值范围;方法二是要使函数f(x)在区间(1,+∞)上是减函数,我们可以转化为f′(x)≤0在区间(1,+∞)上恒成立的问题来求解,然后利用二次函数的单调区间于对称轴的关系来解答也可达到目标.
(2)对参数a进行讨论,然后利用导数f′(x)≤0(注意函数的定义域)来解答,方法一是先解得单调减区间A,再与已知条件中的减区间(1,+∞)比较,即只需要(1,+∞)⊆A即可解答参数的取值范围;方法二是要使函数f(x)在区间(1,+∞)上是减函数,我们可以转化为f′(x)≤0在区间(1,+∞)上恒成立的问题来求解,然后利用二次函数的单调区间于对称轴的关系来解答也可达到目标.
解答:解:(1)当a=1时,f(x)=lnx-x2+x,其定义域是(0,+∞),---------(1分)
∴f′(x)=
-2x+1=-
-------------------(2分)
令f'(x)=0,即-
=0,解得x=-
或x=1.
∵x>0,∴x=-
舍去.
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
∴函数f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减
∴当x=1时,函数f(x)取得最大值,其值为f(1)=ln1-12+1=0.---(6分)
(2)法一:因为f(x)=lnx-a2x2+ax其定义域为(0,+∞),
所以f′(x)=
-2a2x+a=
=
①当a=0时,f′(x)=
>0,
∴f(x)在区间(0,+∞)上为增函数,不合题意----------(8分)
②当a>0时,f'(x)<0(x>0)等价于(2ax+1)(ax-1)>0(x>0),即x>
.
此时f(x)的单调递减区间为(
,+∞).
依题意,得
解之得a≥1.-------------------(12分)
③当a<0时,f'(x)<0(x>0)等价于(2ax+1)(ax-1)>(x>0),即x>
•
此时f(x)的单调递减区间为(-
,+∞),
∴
得a≤-
(14分)
综上,实数a的取值范围是(-∞,-
]∪[1,+∞)-----------(16分)
法二:∵f(x)=lnx-a2x2+ax,x∈(0,+∞)
∴f′(x)=
由f(x)在区间(1,+∞)上是减函数,可得-2a2x2+ax+1≤0在区间(1,+∞)上恒成立.--------------8分
①当a=0时,1≤0不合题意----------------------------------10
②当a≠0时,可得
即
∴
-----------14分
∴a∈(-∞,-
]∪[1,+∞)----------------------------------16分
∴f′(x)=
| 1 |
| x |
| 2x2-x-1 |
| x |
令f'(x)=0,即-
| 2x2-x-1 |
| x |
| 1 |
| 2 |
∵x>0,∴x=-
| 1 |
| 2 |
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
∴函数f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减
∴当x=1时,函数f(x)取得最大值,其值为f(1)=ln1-12+1=0.---(6分)
(2)法一:因为f(x)=lnx-a2x2+ax其定义域为(0,+∞),
所以f′(x)=
| 1 |
| x |
| -2a2x2+ax+1 |
| x |
| -(2ax+1)(ax-1) |
| x |
①当a=0时,f′(x)=
| 1 |
| x |
∴f(x)在区间(0,+∞)上为增函数,不合题意----------(8分)
②当a>0时,f'(x)<0(x>0)等价于(2ax+1)(ax-1)>0(x>0),即x>
| 1 |
| a |
此时f(x)的单调递减区间为(
| 1 |
| a |
依题意,得
|
③当a<0时,f'(x)<0(x>0)等价于(2ax+1)(ax-1)>(x>0),即x>
| 1 |
| 2a |
此时f(x)的单调递减区间为(-
| 1 |
| 2a |
∴
|
| 1 |
| 2 |
综上,实数a的取值范围是(-∞,-
| 1 |
| 2 |
法二:∵f(x)=lnx-a2x2+ax,x∈(0,+∞)
∴f′(x)=
| -2a2x2+ax+1 |
| x |
由f(x)在区间(1,+∞)上是减函数,可得-2a2x2+ax+1≤0在区间(1,+∞)上恒成立.--------------8分
①当a=0时,1≤0不合题意----------------------------------10
②当a≠0时,可得
|
|
∴
|
∴a∈(-∞,-
| 1 |
| 2 |
点评:本题以函数为载体,综合考查利用函数的导数来解决有关函数的单调性、最值等问题的能力,考查已知函数的单调性的条件下怎样求解参数的范围问题,考查分类讨论,函数与方程,配方法等数学思想与方法.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
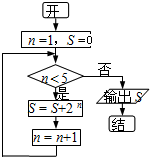 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )