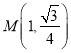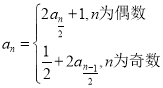题目内容
【题目】设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)当![]() 时,若
时,若![]() 为整数,且
为整数,且![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ,
,![]() ,(Ⅱ)2
,(Ⅱ)2
【解析】
(Ⅰ)根据导数的几何意义,列方程组 ,求解即可.
,求解即可.
(Ⅱ)将![]() 变形整理为
变形整理为![]() ,即
,即![]() (
(![]() ),令
),令![]() ,
, ,令
,令![]() ,则
,则![]() ,函数
,函数![]() 在
在![]() 单调递增,从而确定
单调递增,从而确定![]() 在
在![]() 存在唯一的零点,设此零点为
存在唯一的零点,设此零点为![]() ,则
,则![]() 并且
并且![]() ,即
,即![]() ,再判断
,再判断![]() 的单调性,确定
的单调性,确定![]() 在
在![]() 的最小值为
的最小值为![]() ,求解
,求解![]() 的最大值即可.
的最大值即可.
(Ⅰ)由![]() ,
,
由于![]() 的斜率为1,且过点
的斜率为1,且过点![]() 得,
得,
 即
即![]() 解得
解得![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知![]()
所以![]() 得,
得,![]() .
.
故当![]() 时,等价于
时,等价于![]() (
(![]() )①
)①
令![]() ,则
,则
令![]() ,∵
,∵![]() ,∴
,∴![]()
所以函数![]() 在
在![]() 单调递增.
单调递增.
而![]() ,
,![]() ,所以
,所以![]() 在
在![]() 存在唯一的零点
存在唯一的零点
故![]() 在
在![]() 存在唯一的零点,设此零点为
存在唯一的零点,设此零点为![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 减函数;
减函数;
当![]() 时,
时,![]() ,
,![]() 增函数;
增函数;
所以![]() 在
在![]() 的最小值为
的最小值为![]() ,
,
又由![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
故①等价于![]() ,故整数
,故整数![]() 的最大值为2.
的最大值为2.

练习册系列答案
相关题目