Question

（本小题满分12分）

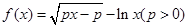已知函数是增函数.

（I）求实数p的取值范围；

（II）设数列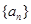的通项公式为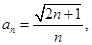前n项和为S，求证：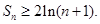

 

Answer 1

【答案】

⑴ 为所求. ⑵证明：见解析。

【解析】（Ｉ）由函数是增函数知对恒成立，

然后采用换元法令，则，然后再求的最大值即可．

（II）由⑴知，是增函数，所以，即，对恒成立. 注意到，所以.

从而可得

从而问题得证．

⑴解：由题意，函数的定义域为，由函数是增函数知对恒成立，                  … 3分  

令，则，注意到，所以 ， 即，所以为所求. ………6分 

⑵证明：由⑴知，是增函数，所以，即，对恒成立. ………… 8分

注意到，所以.  ……10分

即成立……12分