题目内容
数列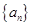 的前
的前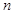 项和记为
项和记为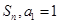 ,
,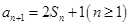
(Ⅰ)求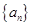 的通项公式;
的通项公式;
(Ⅱ)等差数列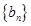 的各项为正,其前
的各项为正,其前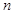 项和为
项和为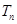 ,且
,且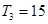 ,又
,又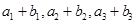 成等比数列,求
成等比数列,求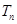 .
.
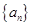 的前
的前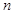 项和记为
项和记为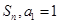 ,
,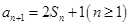
(Ⅰ)求
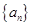 的通项公式;
的通项公式;(Ⅱ)等差数列
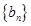 的各项为正,其前
的各项为正,其前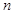 项和为
项和为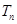 ,且
,且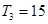 ,又
,又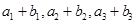 成等比数列,求
成等比数列,求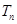 .
.(1)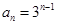 ;(2)
;(2)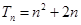 .
.
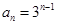 ;(2)
;(2)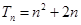 .
.本试题主要考查了舒蕾的通项公式和求和的运用。第一问中利用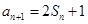 ,得到
,得到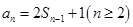 ,两式相减得
,两式相减得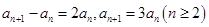 ,故可知故
,故可知故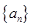 是首项为
是首项为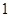 、公比为
、公比为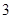 的等比数列, ∴
的等比数列, ∴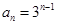
(2)中利用由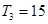 得,可得
得,可得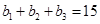 ,可得
,可得 故可设
故可设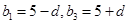 ,解得
,解得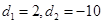 ,利用等差数列的前n项和公式可知∵等差数列
,利用等差数列的前n项和公式可知∵等差数列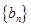 的各项为正,∴
的各项为正,∴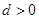 , ∴
, ∴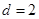
∴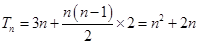
解:(Ⅰ)由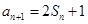 可得
可得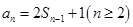 ,
,
两式相减得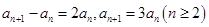
又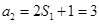 , ∴
, ∴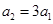
故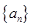 是首项为
是首项为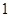 、公比为
、公比为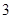 的等比数列, ∴
的等比数列, ∴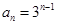
(Ⅱ)设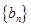 的公比为
的公比为 ,由
,由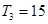 得,可得
得,可得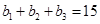 ,可得
,可得
故可设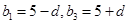 , 又
, 又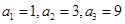
由题意可得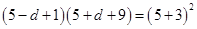 ,解得
,解得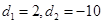
∵等差数列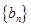 的各项为正,∴
的各项为正,∴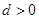 , ∴
, ∴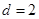
∴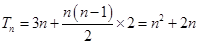
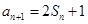 ,得到
,得到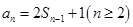 ,两式相减得
,两式相减得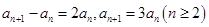 ,故可知故
,故可知故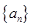 是首项为
是首项为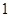 、公比为
、公比为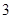 的等比数列, ∴
的等比数列, ∴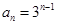
(2)中利用由
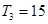 得,可得
得,可得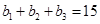 ,可得
,可得 故可设
故可设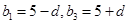 ,解得
,解得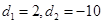 ,利用等差数列的前n项和公式可知∵等差数列
,利用等差数列的前n项和公式可知∵等差数列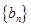 的各项为正,∴
的各项为正,∴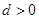 , ∴
, ∴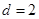
∴
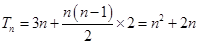
解:(Ⅰ)由
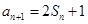 可得
可得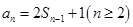 ,
,两式相减得
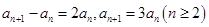
又
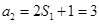 , ∴
, ∴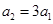
故
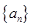 是首项为
是首项为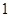 、公比为
、公比为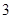 的等比数列, ∴
的等比数列, ∴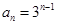
(Ⅱ)设
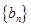 的公比为
的公比为 ,由
,由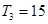 得,可得
得,可得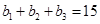 ,可得
,可得
故可设
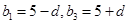 , 又
, 又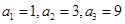
由题意可得
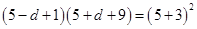 ,解得
,解得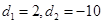
∵等差数列
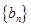 的各项为正,∴
的各项为正,∴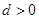 , ∴
, ∴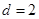
∴
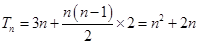

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
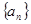 满足
满足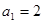 ,
,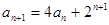
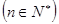 .
. 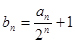 ,求证:数列
,求证:数列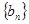 为等比数列;
为等比数列;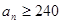 的最小正整数
的最小正整数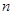 .
.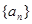 的首项为3,
的首项为3,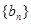 为等差数列且
为等差数列且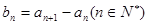 .若
.若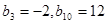 ,则
,则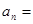 ( )
( ) 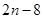
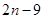
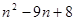
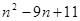
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式.
,求Tn的表达式.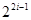 ( i≥1).
( i≥1).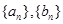 的前n项和分别为
的前n项和分别为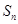 和
和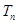 ,若
,若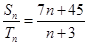 ,且
,且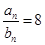 ,则n的值为__________.
,则n的值为__________.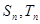 分别是等差数列
分别是等差数列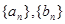 的前
的前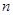 项和,且
项和,且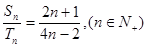 则
则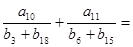
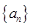 中,
中,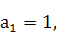 d="0," 则a2012 = ____
d="0," 则a2012 = ____ 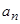 }中,
}中,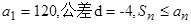 (
(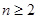 ),则
),则