题目内容
3.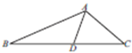 如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
分析 利用已知由余弦定理可求cos∠BAC的值,可求sin$∠BAC=\frac{\sqrt{15}}{4}$,利用两角差的正弦函数公式即可求sin∠CAD=sin(∠BAC-∠BAD)的值.
解答 解:∵AB=3,AC=2,BC=4,
∴由余弦定理可得:cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{9+4-16}{2×3×2}$=-$\frac{1}{4}$,
∴知sin$∠BAC=\frac{\sqrt{15}}{4}$,sin∠CAD=sin(∠BAC-∠BAD)=$\frac{\sqrt{15}}{4}$×$\frac{\sqrt{3}}{2}$-(-$\frac{1}{4}$)×$\frac{1}{2}$=$\frac{3\sqrt{5}+1}{8}$.
故答案为:$\frac{3\sqrt{5}+1}{8}$.
点评 本题主要考查了余弦定理,两角差的正弦函数公式的综合应用,属于基本知识的考查.

练习册系列答案
相关题目
8.在复平面内,复数z满足(2-i)•z=i3(i为虚数单位),则复数z表示的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.有1000个形状相同的球,其中红球500个,黄球300个,绿球200个,采用按颜色分层抽样的方法随机抽取100个球进行分析,则应抽取红球的个数为( )
| A. | 20个 | B. | 30个 | C. | 50个 | D. | 100个 |
13.已知一次函数f(x)=ax+b,满足f(2)=0,f(-2)=1,则f(4)=( )
| A. | $\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 1 |
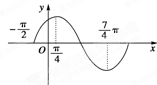 函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求:
函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求: