题目内容
函数 的部分图像如图所示,
的部分图像如图所示,

(Ⅰ)求出函数 的解析式;
的解析式;
(Ⅱ)若 ,求
,求 的值。
的值。
 的部分图像如图所示,
的部分图像如图所示,
(Ⅰ)求出函数
 的解析式;
的解析式;(Ⅱ)若
 ,求
,求 的值。
的值。(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)求出函数
 的解析式,由图像求三角函数的解析式,主要观察特殊点,一是最值点,它决定振幅
的解析式,由图像求三角函数的解析式,主要观察特殊点,一是最值点,它决定振幅 ,二是,最大值与最小值或与
,二是,最大值与最小值或与 轴的交点与最值点的横坐标之差,它决定周期,从而决定
轴的交点与最值点的横坐标之差,它决定周期,从而决定 ,三是观察相位,它决定
,三是观察相位,它决定 ,本题最小值为-2,与
,本题最小值为-2,与 轴的交点与最小值点的横坐标之差为
轴的交点与最小值点的横坐标之差为 ,
, 取得最小值,有这些条件可以求出
取得最小值,有这些条件可以求出 的值从而得
的值从而得 的解析式;(Ⅱ)由
的解析式;(Ⅱ)由 ,可求出
,可求出 ,又因为
,又因为 ,可得
,可得 ,求
,求 的值,需对它进行化简,恒等变形,恒等变形遵循的原则是切割化弦,化高次为低次,化复角为单角,或向已知条件靠拢,本题最终化为
的值,需对它进行化简,恒等变形,恒等变形遵循的原则是切割化弦,化高次为低次,化复角为单角,或向已知条件靠拢,本题最终化为 ,从而求解.
,从而求解.试题解析:(Ⅰ)
 ,由图像得到
,由图像得到 ,将
,将 代入
代入
 (6分)
(6分)(Ⅱ)
 (8分)
(8分)


练习册系列答案
相关题目
 cosx,cosx),设函数f(x)=a•b-
cosx,cosx),设函数f(x)=a•b- , 且α∈(
, 且α∈( ,π). 求α.
,π). 求α. .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 上的最大值与最小值的和为
上的最大值与最小值的和为 ,求
,求 的值.
的值.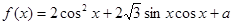 ,且当
,且当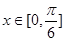 时,
时,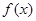 的最小值为2.
的最小值为2.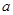 的值,并求
的值,并求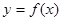 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的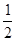 倍,再把所得图象向右平移
倍,再把所得图象向右平移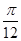 个单位,得到函数
个单位,得到函数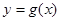 ,求方程
,求方程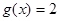 在区间
在区间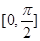 上的所有根之和.
上的所有根之和. 在
在 的图像大致为( )
的图像大致为( )
 ;(2)图像关于直线
;(2)图像关于直线 对称;(3)在
对称;(3)在 上是增函数”的一个函数是( )
上是增函数”的一个函数是( )



 的图象按向量
的图象按向量 平移,再把所得图象上各点的横坐标缩短为原来的
平移,再把所得图象上各点的横坐标缩短为原来的 ,则所得图象的函数解析式是( )
,则所得图象的函数解析式是( )



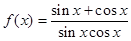 ,在下列给出结论中:
,在下列给出结论中: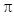 是
是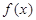 的一个周期;
的一个周期;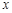
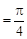 对称;
对称; 上单调递减.
上单调递减. ,
, ,在
,在 中,正数的个数是
中,正数的个数是



