题目内容
将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:①面DBC是等边三角形; ②AC⊥BD; ③三棱锥D-ABC的体积是
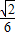 .
.其中正确命题的个数为( )
A.0
B.1
C.2
D.3
【答案】分析:先作出图来,①根据图可知BD=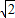 DO=1,再由BC=DC=1,可知面DBC是等边三角形.
DO=1,再由BC=DC=1,可知面DBC是等边三角形.
②由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD.
③三棱锥D-ABC的体积= S△ABC•OD=
S△ABC•OD= •
• •1•1•
•1•1•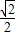 =
=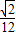 .
.
解答: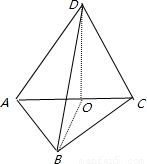 解:如图所示:BD=
解:如图所示:BD=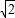 DO=
DO=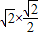 =1
=1
又BC=DC=1
∴面DBC是等边三角形①正确;
∵AC⊥DO,AC⊥BO
∴AC⊥平面DOB
∴AC⊥BD
②正确;
三棱锥D-ABC的体积= S△ABC•OD=
S△ABC•OD= •
• •1•1•
•1•1•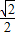 =
=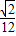 ,
,
③不正确.
故选C.
点评:本题主要考查折叠问题,要注意折叠前后的改变的量和位置,不变的量和位置,属中档题.
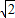 DO=1,再由BC=DC=1,可知面DBC是等边三角形.
DO=1,再由BC=DC=1,可知面DBC是等边三角形.②由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD.
③三棱锥D-ABC的体积=
 S△ABC•OD=
S△ABC•OD= •
• •1•1•
•1•1•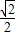 =
=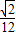 .
.解答:
 解:如图所示:BD=
解:如图所示:BD=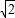 DO=
DO=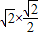 =1
=1又BC=DC=1
∴面DBC是等边三角形①正确;
∵AC⊥DO,AC⊥BO
∴AC⊥平面DOB
∴AC⊥BD
②正确;
三棱锥D-ABC的体积=
 S△ABC•OD=
S△ABC•OD= •
• •1•1•
•1•1•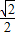 =
=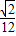 ,
,③不正确.
故选C.
点评:本题主要考查折叠问题,要注意折叠前后的改变的量和位置,不变的量和位置,属中档题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起,使得点A到点A′的位置,且A′C=1,则折起后二面角A′-DC-B的大小( )
A、arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
 将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足
将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|