Question

已知定义在(0,+∞)上的函数f(x)满足①x＞1时,f(x)＜0;②f()=1;③对任意的x、y∈(0,+∞),都有f(xy)=f(x)+f(y).求不等式f(x)+f(5-x)≥-2的解集.

Answer 1

解：需先研究y=f(x)的单调性,任取x₁、x₂∈(0,+∞)且x₁＞x₂,则＞1.

    f(x₁)=f(·x₂)=f()+f(x₂),

    ∴f(x₁)-f(x₂)=f()＜0.

    ∴f(x)在(0,+∞)上为减函数.

    又f(1)=f(1)+f(1),则f(1)=0.

    又∵f(1)=f(2)+f()=f(2)+1=0,

    ∴f(2)=-1.

    ∴f(4)=2f(2)=-2.

    ∴原不等式等价于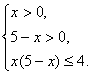

    解得{x|0＜x≤1或4≤x＜5}.