题目内容
已知函数f(x)=2n(1)求数列{an}的通项公式;
(2)证明![]() +
+![]() +…+
+…+![]() <
<![]() ;
;
(3)在点列An(2n,an)中是否存在两点Ai、Aj(i、j∈N*),使直线AiAj的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
(1)解:由f(x)=2n![]() -x,得f′(x)=
-x,得f′(x)=![]() -1.
-1.
令f′(x)=0,得x=![]() .
.
当x∈(0,![]() )时,f′(x)<0;
)时,f′(x)<0;
当x∈(![]() ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.
∴f(x)在[0,+∞]上,当x=![]() 时取得最小值
时取得最小值![]() .
.
∴an=![]() .
.
(2)证明:∵![]() =
=![]() =
=![]() (
(![]() -
-![]() ),
),
∴![]() +
+![]() +…+
+…+![]()
=![]() [(1-
[(1-![]() )+(
)+(![]() -
-![]() )+…+(
)+…+(![]() -
-![]() )]
)]
=![]() (1-
(1-![]() )<
)<![]() .
.
(3)解:不存在.
设Ai(2i,ai)、Aj(2j,aj)(其中i、j∈N*),
则![]() =
=![]() =
=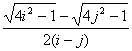 =
=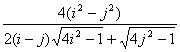 .
.
又![]() >
>![]() =1,故不存在.
=1,故不存在.

练习册系列答案
相关题目