题目内容
已知:数列{an}的前n项和为Sn,且满足Sn=2an-n,(n∈N*).
(Ⅰ)求:a1,a2的值;
(Ⅱ)求:数列{an}的通项公式;
(Ⅲ)若数列{bn}的前n项和为Tn,且满足bn=nan,(n∈N*),求数列{bn}的前n项和Tn.
解:(Ⅰ)∵Sn=2an-n,
令n=1,解得a1=1;
令n=2,解得a2=3 …(2分)
(Ⅱ)∵Sn=2an-n,
所以Sn-1=2an-1-(n-1),(n≥2)
两式相减得 an=2an-1+1 …(4分)
所以an+1=2(an-1+1),(n≥2)…(5分)
又因为a1+1=2
所以数列{an+1}是首项为2,公比为2的等比数列 …(6分)
所以 ,即通项公式
,即通项公式 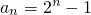 …(7分)
…(7分)
(Ⅲ)∵bn=nan,
所以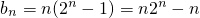
所以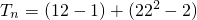 +…+(n•2n-n)
+…+(n•2n-n)
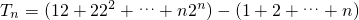 …(9分)
…(9分)
令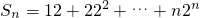 ①
①
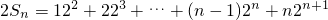 ②
②
①-②得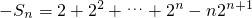
=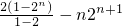 …(11分)
…(11分)
∴ =2+(n-1)•2n+1 …(12分)
=2+(n-1)•2n+1 …(12分)
所以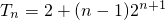
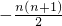 …(13分)
…(13分)
分析:(Ⅰ)由Sn=2an-n,分别令n=1,2可求a1,a2,
(Ⅱ)由Sn=2an-n,可知Sn-1=2an-1-(n-1),(n≥2),两式相减可得 an与an-1的关系,构造等比数列即可求解an+1,然后求出an
(Ⅲ)由bn=nan,结合 数列的特点可利用分组求和,然后利用等差数列的求和及错位相减求和即可
点评:本题主要考查了利用数列的递推公式构造等比数列求解数列的通项公式,分组求和方法及错位相减求和方法的综合应用.
令n=1,解得a1=1;
令n=2,解得a2=3 …(2分)
(Ⅱ)∵Sn=2an-n,
所以Sn-1=2an-1-(n-1),(n≥2)
两式相减得 an=2an-1+1 …(4分)
所以an+1=2(an-1+1),(n≥2)…(5分)
又因为a1+1=2
所以数列{an+1}是首项为2,公比为2的等比数列 …(6分)
所以
 ,即通项公式
,即通项公式 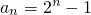 …(7分)
…(7分)(Ⅲ)∵bn=nan,
所以
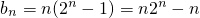
所以
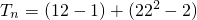 +…+(n•2n-n)
+…+(n•2n-n)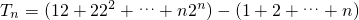 …(9分)
…(9分)令
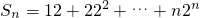 ①
①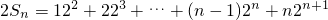 ②
②①-②得
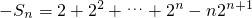
=
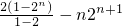 …(11分)
…(11分)∴
 =2+(n-1)•2n+1 …(12分)
=2+(n-1)•2n+1 …(12分)所以
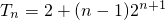
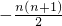 …(13分)
…(13分)分析:(Ⅰ)由Sn=2an-n,分别令n=1,2可求a1,a2,
(Ⅱ)由Sn=2an-n,可知Sn-1=2an-1-(n-1),(n≥2),两式相减可得 an与an-1的关系,构造等比数列即可求解an+1,然后求出an
(Ⅲ)由bn=nan,结合 数列的特点可利用分组求和,然后利用等差数列的求和及错位相减求和即可
点评:本题主要考查了利用数列的递推公式构造等比数列求解数列的通项公式,分组求和方法及错位相减求和方法的综合应用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目