题目内容
已知抛物线C的顶点是椭圆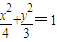 的中心,且焦点与该椭圆右焦点重合.
的中心,且焦点与该椭圆右焦点重合.(Ⅰ)求抛物线C的方程;
(Ⅱ)若P(a,0)为x轴上一动点,过P点作直线交抛物线C于A、B两点.
(ⅰ)设S△AOB=t•tan∠AOB,试问:当a为何值时,t取得最小值,并求此最小值.
(ⅱ)若a=-1,点A关于x轴的对称点为D,证明:直线BD过定点.
【答案】分析:(Ⅰ)由题意,设抛物线C的标准方程为y2=2px(x>0),焦点F( ,0),由椭圆
,0),由椭圆 的右焦点为(1,0),知p=2,由此能求出抛物线方程.
的右焦点为(1,0),知p=2,由此能求出抛物线方程.
(Ⅱ)(ⅰ)设直线AB:my=x-a.联立 ,得
,得 =0,由此能推导出当a=2时,t有最小值一2.
=0,由此能推导出当a=2时,t有最小值一2.
(ⅱ)由(ⅰ)知D(x1,-y1),y1+y2=4m,y1y2=4,直线BD的方程为 ,由此能导出直线BD过定点(1,0).
,由此能导出直线BD过定点(1,0).
解答:解:(Ⅰ)由题意,设抛物线C的标准方程为y2=2px(x>0),焦点F( ,0),
,0),
∵椭圆 的右焦点为(1,0),
的右焦点为(1,0),
∴ ,即p=2,
,即p=2,
∴抛物线方程为:y2=4x,…(4分)
(Ⅱ)(ⅰ)设直线AB:my=x-a.
联立 ,消x得
,消x得 =0,
=0,
设A(x1,y1),B(x2,y2),则y1y2=-4a, ,…(6分)
,…(6分)
由S△AOB=
= ,
,
∴ ,
,
∵ ,…(8分)
,…(8分)
∴ ,
,
∴当a=2时,t有最小值一2.…(10分)
(ⅱ)由(ⅰ)可知D(x1,-y1),y1+y2=4m,y1y2=4,
直线BD的方程为y-y2= ,
,
即
y=
∴y= ,
,
∴直线BD过定点(1,0).…(14分)
点评:本题考查抛物线方程的求法,考查最小值的求法,考查直线过定点的判断,解题时要认真审题,注意等价转化思想的合理运用.
 ,0),由椭圆
,0),由椭圆 的右焦点为(1,0),知p=2,由此能求出抛物线方程.
的右焦点为(1,0),知p=2,由此能求出抛物线方程.(Ⅱ)(ⅰ)设直线AB:my=x-a.联立
 ,得
,得 =0,由此能推导出当a=2时,t有最小值一2.
=0,由此能推导出当a=2时,t有最小值一2.(ⅱ)由(ⅰ)知D(x1,-y1),y1+y2=4m,y1y2=4,直线BD的方程为
 ,由此能导出直线BD过定点(1,0).
,由此能导出直线BD过定点(1,0).解答:解:(Ⅰ)由题意,设抛物线C的标准方程为y2=2px(x>0),焦点F(
 ,0),
,0),∵椭圆
 的右焦点为(1,0),
的右焦点为(1,0),∴
 ,即p=2,
,即p=2,∴抛物线方程为:y2=4x,…(4分)
(Ⅱ)(ⅰ)设直线AB:my=x-a.
联立
 ,消x得
,消x得 =0,
=0,设A(x1,y1),B(x2,y2),则y1y2=-4a,
 ,…(6分)
,…(6分)由S△AOB=

=
 ,
,∴
 ,
,∵
 ,…(8分)
,…(8分)∴
 ,
,∴当a=2时,t有最小值一2.…(10分)
(ⅱ)由(ⅰ)可知D(x1,-y1),y1+y2=4m,y1y2=4,
直线BD的方程为y-y2=
 ,
,即

y=

∴y=
 ,
,∴直线BD过定点(1,0).…(14分)
点评:本题考查抛物线方程的求法,考查最小值的求法,考查直线过定点的判断,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
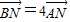 ,求直线AB的方程.
,求直线AB的方程.