题目内容
已知函数f(x)=| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(1)求f(θ)的值
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 4 |
分析:(1)直接对原函数化简整理,再把点(
,
)的坐标代入求出θ即可求f(θ)的值;
(2)先根据图象的平移变换规律求出函数y=g(x)的解析式,再根据x的范围画出图象,结合图象即可求出实数k的取值范围.
| π |
| 6 |
| 1 |
| 2 |
(2)先根据图象的平移变换规律求出函数y=g(x)的解析式,再根据x的范围画出图象,结合图象即可求出实数k的取值范围.
解答:解:(1)因为f(x)=
sin2xsinθ+
cosθ-
cosθ=
(sin2xsinθ+cos2xcosθ)
=
cos(2x-θ)…(3分)
由f(
)=
得cos(
-θ)=1
∴
-θ=2kπ又θ∈(0,π),
∴θ=
…(5分)
∴f(θ)=
cosθ=
…(6分)
(2)因为函数y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,
得到函数y=g(x)=
cos(4x-
)…(8分)
当x∈[0,
]时,4x-
∈[-
,
],
作出y=
cost在t∈[-
,
]的图象,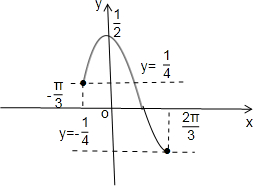
结合图形知k=
或-
<k<
.…(12分)
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
由f(
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
∴
| π |
| 3 |
∴θ=
| π |
| 3 |
∴f(θ)=
| 1 |
| 2 |
| 1 |
| 4 |
(2)因为函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
得到函数y=g(x)=
| 1 |
| 2 |
| π |
| 3 |
当x∈[0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
作出y=
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
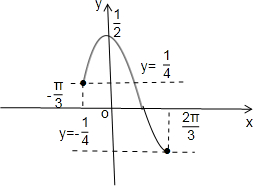
结合图形知k=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查三角函数的图象变换以及三角函数式的整理化简.在整理三角函数式时,要牢记公式,并会对公式熟练使用.

练习册系列答案
相关题目