题目内容
△ABC的三内角的正弦值的比为4:5:6,则三角形的最大角为________.

分析:先由正弦定理得出三内角的正弦值比值即等于三条边的比值,可设三边分别为4k、5k、6k,再根据大边对大角,得出边长为6k的边所对的角为三角形的最大角,再用余弦定理计算出此角的余弦值.
解答:由正弦定理得:△ABC三边的比为4:5:6,不妨设a=4k,b=5k,c=6k,(k>0)
则边c所对的角C为最大角,cosC=
 =
= ,∴C=arccos
,∴C=arccos .
.故答案为:

点评:本题主要考查了正弦定理与余弦定理相结合在解三角形中的应用,属于简单题.

练习册系列答案
相关题目
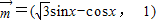 ,
,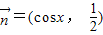 ,若
,若 .
.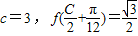 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.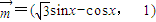 ,
,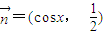 ,若
,若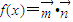 .
.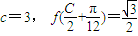 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值. ,
, ,若
,若 .
. (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.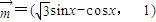 ,
,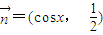 ,若
,若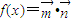 .
.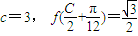 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.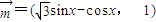 ,
,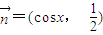 ,若
,若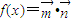 .
.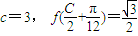 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.