题目内容
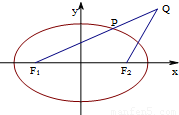
已知椭圆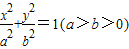 的左右焦点为F1(-c,0),F2(c,0),点Q是椭圆外的动点,满足|
的左右焦点为F1(-c,0),F2(c,0),点Q是椭圆外的动点,满足|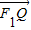 |=2a,点P是线段F1Q与该椭圆的交点,曲线C的方程是x2+y2=a2
|=2a,点P是线段F1Q与该椭圆的交点,曲线C的方程是x2+y2=a2(1)若点P的横坐标为
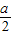 ,证明:|
,证明:|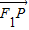 |=a+
|=a+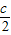
(2)试问:曲线C上是否存在点M,使得△F1MF2的面积等于S=b2?若存在,求出椭圆离心率的取值范围;若不存在,请说明理由.
【答案】分析:(1)确定椭圆的左准线方程,利用椭圆的定义,可得 ,从而可得结论;
,从而可得结论;
(2)利用存在点M,使得△F1MF2的面积等于b2,确定M的纵坐标,即可求椭圆离心率的取值范围.
解答:(1)证明:椭圆 的左准线方程为
的左准线方程为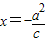
∵点P的横坐标为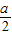 ,
,
∴由椭圆的定义可知,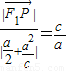 ,
,
∴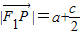 ;
;
(2)解:假设存在,设M(x,y),则
∵△F1MF2的面积等于S=b2,
∴
∴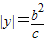
∵M在x2+y2=a2上,
∴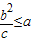
∴e2+e-1≥0
∴e≥ 或e≤-
或e≤-
∵0<e<1
∴ .
.
点评:本题考查椭圆的定义,考查椭圆的性质,考查学生分析解决问题的能力,属于中档题.
 ,从而可得结论;
,从而可得结论;(2)利用存在点M,使得△F1MF2的面积等于b2,确定M的纵坐标,即可求椭圆离心率的取值范围.
解答:(1)证明:椭圆
 的左准线方程为
的左准线方程为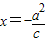
∵点P的横坐标为
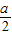 ,
,∴由椭圆的定义可知,
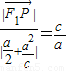 ,
,∴
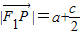 ;
;(2)解:假设存在,设M(x,y),则
∵△F1MF2的面积等于S=b2,
∴

∴
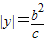
∵M在x2+y2=a2上,
∴
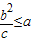
∴e2+e-1≥0
∴e≥
 或e≤-
或e≤-
∵0<e<1
∴
 .
.点评:本题考查椭圆的定义,考查椭圆的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的左右焦点为
的左右焦点为 ;直线
;直线 经过
经过 交椭圆于
交椭圆于 两点.
两点.
 的周长为定值.
的周长为定值. 的左右焦点为
的左右焦点为 ,直线AB过点
,直线AB过点 且交椭圆于A、B两点,则△
且交椭圆于A、B两点,则△ 的周长为_____________
的周长为_____________ 的左右焦点为
的左右焦点为 ,过点
,过点 且斜率为正数的直线
且斜率为正数的直线 交椭圆
交椭圆 于
于 两点,且
两点,且 成等差数列。
成等差数列。 与椭圆
与椭圆 两点,求使四边形
两点,求使四边形 的面积最大时的
的面积最大时的 值。
值。 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: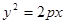 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。 的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )
的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( ) B.3 C.
B.3 C. D.
D.