题目内容
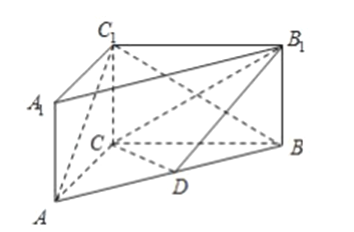
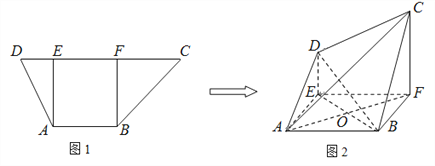
【题目】以边长为4的等比三角形![]() 的顶点
的顶点![]() 以及
以及![]() 边的中点
边的中点![]() 为左、右焦点的椭圆过
为左、右焦点的椭圆过![]() 两点.
两点.
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点,求证直线
两点,求证直线![]() 与
与![]() 的交点在一条直线上.
的交点在一条直线上.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)先建立直角坐标系,使椭圆方程为标准方程,则![]()
(2)研究圆锥曲线的定值问题,一般方法为以算代证,即先求两直线交点坐标,再确定交点所在定直线:由对称性可知两直线交点必在垂直于x轴的直线上,因此运算目标为求交点横坐标为定值,设![]() 的方程为
的方程为![]() ,
, ![]() ,则
,则![]() :
: ![]() ,
, ![]() :
: ![]() ,消去y得
,消去y得![]() ,再利用直线方程与椭圆方程联立方程组,结合韦达定理可得
,再利用直线方程与椭圆方程联立方程组,结合韦达定理可得![]() ,
, ![]() ,代入化简得
,代入化简得![]()
试题解析:(1) 由题意可知两焦点为![]() 与
与![]() ,且
,且![]() ,因此椭圆的方程为
,因此椭圆的方程为![]() . (4分)
. (4分)
(2) ① 当![]() 不与
不与![]() 轴重合时,
轴重合时,
设![]() 的方程为
的方程为![]() ,且
,且![]() ,
, ![]()
联立椭圆与直线![]()
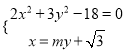 消去
消去![]() 可得
可得![]() ,即
,即![]() ,
, ![]()
设![]() ,
, ![]()
则![]() :
: ![]() ①
①
![]() :
: ![]() ②
②
②-①得
![]()
![]()
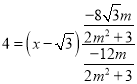
![]()
则![]() ,即
,即![]() .
.
②当![]() 与
与![]() 轴重合时,即
轴重合时,即![]() 的方程为
的方程为![]() ,即
,即![]() ,
, ![]() .
.
即![]() :
: ![]() ①
①
![]() :
: ![]() ②
②
联立①和②消去![]() 可得
可得![]() .
.
综上![]() 与
与![]() 的交点在直线
的交点在直线![]() 上.
上.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目