题目内容
已知函数f(x)=
x3+ax2-bx+1(x∈R,a,b为实数)有极值,且在x=1处的切线与直线x-y+1=0平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数f(x)的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数g(x)=
-2lnx,试判断函数g(x)在(1,+∞)上的符号,并证明:lnn+
(1+
)≤
(n∈N*).
| 1 |
| 3 |
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数f(x)的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数g(x)=
| f′(x)-2ax+b-1 |
| x |
| 1 |
| 2 |
| 1 |
| n |
| n |
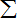 |
| i-1 |
| 1 |
| i |
(Ⅰ)∵f′(x)=x2+2ax-b,∴f′(1)=1+2a-b,
又因为函数在x=1处的切线与直线x-y+1=0平行,所以在x=1处的切线的斜率等于1,∴f′(1)=1∴b=2a①
∵f(x)有极值,故方程f′(x)=x2+2ax-b=0有两个不等实根∴△=4a2+4b>0∴a2+b>0②
由①.②可得,a2+2a>0∴a<-2或a>0
故实数a的取值范围是a∈(-∞,-2)∪(0,+∞)
((Ⅱ)存在a=-
…(5分)
由(1)可知f′(x)=x2+2ax-b,令f′(x)=0∴x1=-a-
,x2=-a+

∴f(x)极小=f(x2)=
x23+ax22-2ax2+1=1,
∴x2=0或x22+3ax2-6a=0
若x2=0,则-a+
=0,则a=0(舍),
若x22+3ax2-6a=0,又f′(x2)=0,∴x22+2ax2-2a=0,
∴ax2-4a=0
∵a≠0∴x2=4
∴-a+
=4,
∴a=-
<2∴存在实数a=-
,使得函数f(x)的极小值为1.
(Ⅲ)由g(x)=
-2lnx=
-2lnx=x-
-2lnx
故g′(x)=1+
-
=
=
>0,
则g(x)在(1,+∞)上是增函数,故g(x)>g(1)=0,
所以,g(x)在(1,+∞)上恒为正.
当n是正整数时,
>1,设x=
,则
g(
)=
-
-2ln
=1+
-1+
-2[ln(n+1)-lnn]
=
+
-2[ln(n+1)-lnn]>0,
即
+
>2[ln(n+1)-lnn]
上式分别取n的值为1、2、3、…、n-1(n>1)累加得:
(
+
)+(
+
)+(
+
)+…+
+
>2[ln2-ln1+ln3-ln2+ln4-ln3+…lnn-ln(n-1)]
∴1+2(
+
+
+…
)+
>2lnn
2(1+
+
+
+…
+
)>2lnn+1+
∴1+
+
+
+…
+
)>lnn+
(1+
)
即lnn+
(1+
)<
,(n>1)
又当n=1时,lnn+
(1+
)=
,
故lnn+
(1+
)≤
,当且仅当n=1时取等号.
又因为函数在x=1处的切线与直线x-y+1=0平行,所以在x=1处的切线的斜率等于1,∴f′(1)=1∴b=2a①
∵f(x)有极值,故方程f′(x)=x2+2ax-b=0有两个不等实根∴△=4a2+4b>0∴a2+b>0②
由①.②可得,a2+2a>0∴a<-2或a>0
故实数a的取值范围是a∈(-∞,-2)∪(0,+∞)
((Ⅱ)存在a=-
| 8 |
| 3 |
由(1)可知f′(x)=x2+2ax-b,令f′(x)=0∴x1=-a-
| a2+2a |
| a2+2a |

∴f(x)极小=f(x2)=
| 1 |
| 3 |
∴x2=0或x22+3ax2-6a=0
若x2=0,则-a+
| a2+2a |
若x22+3ax2-6a=0,又f′(x2)=0,∴x22+2ax2-2a=0,
∴ax2-4a=0
∵a≠0∴x2=4
∴-a+
| a2+2a |
∴a=-
| 8 |
| 3 |
| 8 |
| 3 |
(Ⅲ)由g(x)=
| f′(x)-2ax+b-1 |
| x |
| x2+2ax-b-2ax+b-1 |
| x |
| 1 |
| x |
故g′(x)=1+
| 1 |
| x2 |
| 2 |
| x |
| x2-2x+1 |
| x2 |
| (x-1)2 |
| x2 |
则g(x)在(1,+∞)上是增函数,故g(x)>g(1)=0,
所以,g(x)在(1,+∞)上恒为正.
当n是正整数时,
| n+1 |
| n |
| n+1 |
| n |
g(
| n+1 |
| n |
| n+1 |
| n |
| n |
| n+1 |
| n+1 |
| n |
=1+
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| n |
| 1 |
| n+1 |
即
| 1 |
| n |
| 1 |
| n+1 |
上式分别取n的值为1、2、3、…、n-1(n>1)累加得:
(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
>2[ln2-ln1+ln3-ln2+ln4-ln3+…lnn-ln(n-1)]
∴1+2(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
2(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
∴1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
即lnn+
| 1 |
| 2 |
| 1 |
| n |
| n |
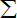 |
| i-1 |
| 1 |
| i |
又当n=1时,lnn+
| 1 |
| 2 |
| 1 |
| n |
| n |
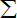 |
| i-1 |
| 1 |
| i |
故lnn+
| 1 |
| 2 |
| 1 |
| n |
| n |
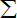 |
| i-1 |
| 1 |
| i |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|