题目内容

已知椭圆
x2
4
+
y2
3
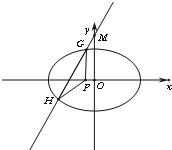
=1，过椭圆的右焦点F的直线l与椭圆交于点A、B，定直线x=4交x轴于点K，直线KA和直线KB的斜率分别是k1、k2．
（1）若直线l的倾斜角是45°，求线段AB的长；
（2）求证：k1+k2=0．
（1）直线l的方程是y=x-1，代入椭圆方程整理得：7x2-8x-8=0
设A（x1，y1），B（x2，y2），则x1+x2=
8
7
，x1x2=-
8
7
．…2分
|AB|=
1+k2
•|x1-x2|=
2
•
(
8
7
)2+
32
7
=
24
7
．…5分
（2）证明：当l⊥x轴时，由椭圆的对称性易知k1+k2=0；…6分
当l不与x轴垂直时，设其方程是：y=k（x-1）代入椭圆方程整理得：（3+4k2）x2-8k2x+4k2-12=0，易知其判别式△＞0恒成立，
设A（x1，y1），B（x2，y2），则x1+x2=
8k2
3+4k2
，x1x2=
4k2-12
3+4k2
．…9分
而K（4，0）
则k1+k2=
y1
x1-4
+
y2
x2-4
=
x1y2+y1x2-4(y1+y2)
(x1-4)(x2-4)
=
k[2x1xx-5(x1+x2)+8]
(x1-4)(x2-4)
=0
即k1+k2=0
综上总有k1+k2=0．…13分
练习册系列答案
相关题目
设抛物线y2=8x的准线与x轴交于点Q，若过Q点的直线l与抛物线有公共点，求直线l的斜率的取值范围．
如图，椭圆C：
x2
4
+
y2
m
=1（0＜m＜4）的左顶点为A，M是椭圆C上异于点A的任意一点，点P与点A关于点M对称．
（1）若点P的坐标为（4，3），求m的值；
（2）若椭圆C上存在点M，使得OP⊥OM，求实数m的最大值．
已知椭圆C：
x2
4
+
y2
3
=1，直线l过点M（m，0）．
（Ⅰ）若直线l交y轴于点N，当m=-1时，MN中点恰在椭圆C上，求直线l的方程；
（Ⅱ）如图，若直线l交椭圆C于A，B两点，当m=-4时，在x轴上是否存在点p，使得△PAB为等边三角形？若存在，求出点p坐标；若不存在，请说明理由．
已知抛物线C：y2=8x，O为坐标原点，动直线l：y=k（x+2）与抛物线C交于不同两点A，B
（1）求证：
OA
•
OB
为常数；
（2）求满足
OM
=
OA
+
OB
的点M的轨迹方程．
椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1（-1，0）、F2（1，0），O是坐标原点，C的右顶点和上顶点分别为A、B，且△AOB的面积为
5
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点P（4，0）作与x轴不重合的直线l与C交于相异两点M、N，交y轴于Q点，证明
|PQ|
|PM|
+
|PQ|
|PN|
为定值，并求这个定值．
已知曲线C：
x2
m+2
+
y2
3-m
=1（m∈R）．
（Ⅰ）若曲线C是焦点在x轴上的椭圆，求m的取值范围；
（Ⅱ）设m=2，过点D（0，4）的直线l与曲线C交于M，N两点，O为坐标原点，若∠OMN为直角，求直线l的斜率．
已知椭圆M：
x2
a2
+
y2
b2
=1(a＞b＞0)经过如下五个点中的三个点：P1(-1，-
2
2
)，P2（0，1），P3(
1
2
，
2
2
)，P4(1，
2
2
)，P5（1，1）．
（Ⅰ）求椭圆M的方程；
（Ⅱ）设点A为椭圆M的左顶点，B，C为椭圆M上不同于点A的两点，若原点在△ABC的外部，且△ABC为直角三角形，求△ABC面积的最大值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，直线l：y=x+2与原点为圆心，以椭圆C的短轴长为直径的圆相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，2）的直线l1与椭圆C交于G，H两点．设直线l1的斜率k＞0，在x轴上是否存在点P（m，0），使得△PGH是以GH为底边的等腰三角形．如果存在，求出实数m的取值范围，如果不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网