题目内容
是否存在实数a,使函数 为奇函数,同时使函数
为奇函数,同时使函数 为偶函数,证明你的结论.
为偶函数,证明你的结论.
解:f(x)为奇函数,所以f(0)=0,
得 .
.
若g(x)为偶函数,则h(x)= 为奇函数,
为奇函数,
h(-x)+h(x)=0

∴存在符合题设条件的a= .
.
分析:因为f(x)为奇函数,g(x)为偶函数,则f(0)=0;分别得到h(x)= 为奇函数,利用f(-x)+f(x)=0得到a的值即可.
为奇函数,利用f(-x)+f(x)=0得到a的值即可.
点评:考查学生对函数奇偶性的应用能力.
得
 .
.若g(x)为偶函数,则h(x)=
 为奇函数,
为奇函数,h(-x)+h(x)=0


∴存在符合题设条件的a=
 .
.分析:因为f(x)为奇函数,g(x)为偶函数,则f(0)=0;分别得到h(x)=
 为奇函数,利用f(-x)+f(x)=0得到a的值即可.
为奇函数,利用f(-x)+f(x)=0得到a的值即可.点评:考查学生对函数奇偶性的应用能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
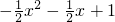 ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;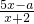 在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.
在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.