题目内容
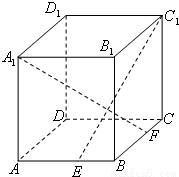
如图,ABCD-A1B1C1D1是四棱柱,底面ABCD是菱形,AA1⊥底面ABCD,AB=2,∠BAD=60°,E是AA1的中点.
(1)求证:平面BD1F⊥平面BB1D1D;
(2)若四面体D1-ABE的体积V=1,求棱柱ABCD-A1B1C1D1的高.
(1)求证:平面BD1F⊥平面BB1D1D;
(2)若四面体D1-ABE的体积V=1,求棱柱ABCD-A1B1C1D1的高.

(1)证明:设平面 ,连接BF,则
,连接BF,则 与△BCF的对应边互相平行,
与△BCF的对应边互相平行,
且 ,所以,
,所以, ,
,
F是CC1的中点,连接 ,
,
因为 底面ABCD,所以,
底面ABCD,所以, ,
, ,
,
ABCD是菱形, ,且
,且 ,所以
,所以 面
面 ,
,
因为E、F分别是 的中点,所以
的中点,所以 是矩形,
是矩形, ,
,
所以EF⊥平面 ,
,
 平面
平面 (即平面
(即平面 ),
),
所以,面 ⊥面
⊥面 。
。
(2)因为 底面ABCD,所以,
底面ABCD,所以, 是棱柱
是棱柱 的高,
的高,
 平面
平面 ,平面
,平面 ⊥底面
⊥底面 ,
,
在底面 上作
上作 ,垂足为F,面
,垂足为F,面 面
面 ,
,
所以, 面
面 ,
,
所以, ,
,
其中, ,
, ,
,
所以, ,
,
解得: ,
,
即棱柱 的高为
的高为 。
。
 ,连接BF,则
,连接BF,则 与△BCF的对应边互相平行,
与△BCF的对应边互相平行,且
 ,所以,
,所以, ,
,F是CC1的中点,连接
 ,
,因为
 底面ABCD,所以,
底面ABCD,所以, ,
, ,
,ABCD是菱形,
 ,且
,且 ,所以
,所以 面
面 ,
,因为E、F分别是
 的中点,所以
的中点,所以 是矩形,
是矩形, ,
,所以EF⊥平面
 ,
, 平面
平面 (即平面
(即平面 ),
),所以,面
 ⊥面
⊥面 。
。(2)因为
 底面ABCD,所以,
底面ABCD,所以, 是棱柱
是棱柱 的高,
的高, 平面
平面 ,平面
,平面 ⊥底面
⊥底面 ,
,在底面
 上作
上作 ,垂足为F,面
,垂足为F,面 面
面 ,
,所以,
 面
面 ,
,所以,
 ,
,其中,
 ,
, ,
,所以,
 ,
,解得:
 ,
,即棱柱
 的高为
的高为 。
。
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
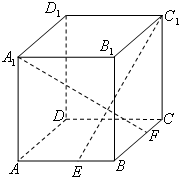 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是