题目内容
在三棱锥P-ABC中, ![]() APB=
APB=![]() BPC=
BPC=![]() CPA=600,求二面角A-PB-C的余弦值。
CPA=600,求二面角A-PB-C的余弦值。
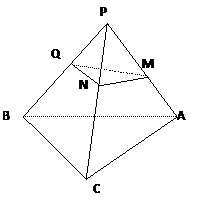
解析:
在二面角的棱PB上任取一点Q,在半平面PBA和半平面PBC上作QM![]() PB,QN
PB,QN![]() PB,则由定义可知
PB,则由定义可知![]() MQN即为二面角的平面角。
MQN即为二面角的平面角。
设PM=a,则在Rt![]() PQM和Rt
PQM和Rt![]() PQN中可求得QM=QN=
PQN中可求得QM=QN=![]() a;
a;
又由![]() PQN
PQN![]()
![]() PQM得PN=a,故在正
PQM得PN=a,故在正![]() PMN中MN=a,在
PMN中MN=a,在![]() MQN中由余弦定理得cos
MQN中由余弦定理得cos![]() MQN=
MQN=![]() ,即二面角的余弦值为
,即二面角的余弦值为![]() 。
。

练习册系列答案
相关题目
题目内容
在三棱锥P-ABC中, ![]() APB=
APB=![]() BPC=
BPC=![]() CPA=600,求二面角A-PB-C的余弦值。
CPA=600,求二面角A-PB-C的余弦值。

在二面角的棱PB上任取一点Q,在半平面PBA和半平面PBC上作QM![]() PB,QN
PB,QN![]() PB,则由定义可知
PB,则由定义可知![]() MQN即为二面角的平面角。
MQN即为二面角的平面角。
设PM=a,则在Rt![]() PQM和Rt
PQM和Rt![]() PQN中可求得QM=QN=
PQN中可求得QM=QN=![]() a;
a;
又由![]() PQN
PQN![]()
![]() PQM得PN=a,故在正
PQM得PN=a,故在正![]() PMN中MN=a,在
PMN中MN=a,在![]() MQN中由余弦定理得cos
MQN中由余弦定理得cos![]() MQN=
MQN=![]() ,即二面角的余弦值为
,即二面角的余弦值为![]() 。
。
