题目内容
若函数
，其中min{p，q}表示p，q两者中的较小者，则f（x）＜2的解为 ________．
0＜x＜4或x＞4
分析：首先按照给出的定义，分①当
时和②当
时两种情况解得函数f（x），然后由分段函数的定义域选择好解析式，用对数函数的单调性求解不等式．
解答：①当时，即0＜x≤4时f（x）=log2x
②当时，即x＞4时，f（x）=
∴
∴当0＜x≤4时，f（x）＜2可转化为：
log2x＜2
解得：0＜x＜4
当0＜x≤4时，f（x）＜2可转化为
＜2
解得：x＞4
综上：0＜x＜4或x＞4
故答案为：0＜x＜4或x＞4
点评：本题主要考查对数不等式的解法，还考查了转化思想，分类讨论思想和运算能力．
分析：首先按照给出的定义，分①当
时和②当时两种情况解得函数f（x），然后由分段函数的定义域选择好解析式，用对数函数的单调性求解不等式．解答：①当
时，即0＜x≤4时f（x）=log2x②当
时，即x＞4时，f（x）=∴
∴当0＜x≤4时，f（x）＜2可转化为：
log2x＜2
解得：0＜x＜4
当0＜x≤4时，f（x）＜2可转化为
＜2解得：x＞4
综上：0＜x＜4或x＞4
故答案为：0＜x＜4或x＞4
点评：本题主要考查对数不等式的解法，还考查了转化思想，分类讨论思想和运算能力．
练习册系列答案
教材全解字词句篇系列答案
相关题目
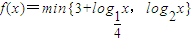，其中min{p，q}表示p，q两者中的较小者，则f(x)＜2的解为________．
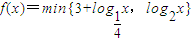，其中min{p，q}表示p，q两者中的较小者，则f（x）＜2的解为 ．
，其中min{p，q}表示p，q两者中的较小者，则f（x）＜2的解为 ．
，其中min{p，q}表示p，q两者中的较小者，则f（x）＜2的解为 （ ）．