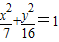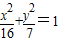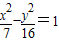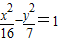题目内容
已知动圆P过定点A（-3,0），并且在定圆B:（x-3）2+y2=64的内部与其相内切，求动圆圆心P的轨迹方程．
思路分析：关键是根据题意，列出点P满足的关系式即|PA|+|PB|=|PM|+|PB|=|BM|=8．
解：如图所示，设动圆P和定圆B内切于点M．动点P到两定点，即定点A（-3,0）和定圆圆心B（3,0）距离之和恰好等于定圆半径，即|PA|+|PB|=|PM|+|PB|=|BM|=8．
∴点P的轨迹是以A,B为两焦点，半长轴为4，半短轴长为b=
的椭圆的方程：
=1．
方法归纳 本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法．
练习册系列答案
相关题目
已知动圆P过定点A（-3，0），并且在定圆B：（x-3）2+y2=64的内部与其相内切，求动圆圆心P的轨迹方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
