题目内容
4.函数f(x)=x3+3x2+3x-a的极值点的个数是( )| A. | 2 | B. | 1 | C. | 0 | D. | 由a确定 |
分析 先求出函数的导数,得到导函数f′(x)≥0,从而得到结论.
解答 解:f′(x)=3x2+6x+3=3(x+1)2≥0,
∴函数f(x)在R上单调递增,
∴函数f(x)=x3+3x2+3x-a的极值点的个数是0个,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
14.不等式x(x+2)≥0的解集为( )
| A. | {x|x≥0或x≤-2} | B. | {x|-2≤x≤0} | C. | {x|0≤x≤2} | D. | {x|x≤0或x≥2} |
15.在△ABC中,若A,B,C所对边的长分别为a,b,c,若a=2,B=$\frac{π}{6}$,c=2$\sqrt{3}$,则b=( )
| A. | 4 | B. | 2 | C. | 16-4$\sqrt{3}$ | D. | 10 |
16.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{asin2x,0≤x≤π}\end{array}\right.$.若方程f(x)=1有3个不同的实数根,则实数a的取值范围是( )
| A. | (1,+∞) | B. | {-1}∪(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
10.设$\overrightarrow a$是非零向量,λ为负实数,下列结论中正确的是( )
| A. | $\overrightarrow a$与$λ\overrightarrow a$的方向相反 | B. | $|{λ\overrightarrow a}|≥|{\overrightarrow a}|$ | ||
| C. | $\overrightarrow a$与${λ^2}\overrightarrow a$的方向相同 | D. | $|{λ\overrightarrow a}|=|λ|\overrightarrow a$ |
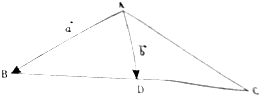 如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.