Question

6．“丁香”和“小花”是好朋友，她们相约本周末去爬歌乐山，并约定周日早上8：00至8：30之间（假定她们在这一时间段内任一时刻等可能的到达）在歌乐山健身步道起点处会合，若“丁香”先到，则她最多等待“小花”15分钟．若“小花”先到，则她最多等待“丁香”10分钟，若在等待时间内对方到达，则她俩就一起快乐地爬山，否则超过等待时间后她们均不再等候对方而孤独爬山，则“丁香”和“小花”快乐地一起爬歌乐山的概率是$\frac{47}{72}$（用数字作答）

Answer 1

分析 由题意知本题是一个几何概型，试验包含的所有事件是Ω={（x，y）|0≤x≤$\frac{1}{2}$，0≤y≤$\frac{1}{2}$}，做出事件对应的集合表示的面积，写出满足条件的事件是A={（x，y）|0≤x≤$\frac{1}{2}$，0≤y≤$\frac{1}{2}$，x-y≤$\frac{1}{4}$，y-x$≤\frac{1}{6}$}，算出事件对应的集合表示的面积，根据几何概型概率公式得到结果

解答 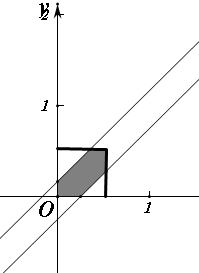解：由题意知本题是一个几何概型，
设“丁香”和“小花”到达的时间分别为（8+x）时、（8+y）时，
则0≤x≤$\frac{1}{2}$，0≤y≤$\frac{1}{2}$，若两人见面，则x-y≤$\frac{15}{60}$=$\frac{1}{4}$，或者y-x$≤\frac{10}{60}=\frac{1}{6}$，
如图，正方形的面积为$\frac{1}{4}$，落在两直线之间部分的面积为$\frac{1}{4}-\frac{1}{18}-\frac{1}{32}$，
∴“丁香”和“小花”快乐地一起爬歌乐山的概率是$\frac{\frac{1}{4}-\frac{1}{18}-\frac{1}{32}}{\frac{1}{4}}=\frac{47}{72}$．
故答案为：$\frac{47}{72}$．

点评 本题是一个几何概型，解答此类问题，一般要通过把试验发生包含的事件同集合结合起来，根据集合对应的图形做出面积，用面积的比值得到结果．