题目内容
已知正方体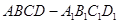 ,点
,点 、
、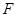 、
、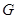 分别是棱
分别是棱 、
、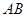 和
和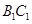 上的动点,观察直线
上的动点,观察直线 与
与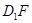 ,
, 与
与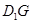 .
.
给出下列结论:
①对于任意点 ,存在点
,存在点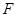 ,使得
,使得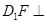
 ;②对于任意点
;②对于任意点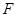 ,存在点
,存在点 ,使得
,使得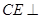
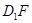 ;
;
③对于任意点 ,存在点
,存在点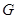 ,使得
,使得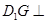
 ;④对于任意点
;④对于任意点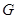 ,存在点
,存在点 ,使得
,使得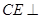
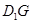 .
.
其中,所有正确结论的序号是__________.
②③
解析试题分析:因为对任意的E点,则直线CE所形成的轨迹都在平面 上,所以要使得
上,所以要使得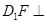
 ,即要存在
,即要存在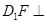 平面
平面 ,显然是不成立的,所以①不正确;因为对于任意点
,显然是不成立的,所以①不正确;因为对于任意点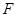 ,由
,由 形成的轨迹在平面
形成的轨迹在平面 上,所以要存在
上,所以要存在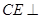
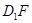 只需要
只需要 即可,这显然可以成立,所以②正确.同理③只要G点移到
即可,这显然可以成立,所以②正确.同理③只要G点移到 点即可成立,所以③正确.与①类似④不成立.故填②③.
点即可成立,所以③正确.与①类似④不成立.故填②③.
考点:1.线面垂直的判定.2.线线垂直的判定.3.线动成面的思维.

练习册系列答案
相关题目

 轴上与点
轴上与点 和点
和点 等距离的点
等距离的点 的坐标为 .
的坐标为 . 是
是 的直径,
的直径, 垂直于
垂直于 是圆周上不同于
是圆周上不同于 的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).



