题目内容
如图2-2-13,△ABC的∠A的外角平分线交△ABC的外接圆于点D.求证:AB +AC＜2BD.
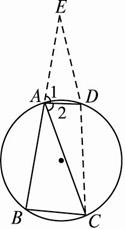
图2-2-13
思路分析:因为比较的是两条线段的和与另一条线段的大小,所以应将两条线段的和转化为一条线段,故可延长BA到E,使得AE =AC,然后比较BE与2BD的大小关系.
证明:在BA延长线上取点E,使得AE=AC.连结DC、DE、BD.?
∵AE =AC,∠1=∠2,AD =AD,?
∴△ADE ≌△ADC.?
∴DE =DC.?
在△BED中,BE＜BD +DE =BD+DC,即AB +AC＜BD +DC.??
∵四边形ABCD是圆内接四边形,∴∠1=∠BCD.?
又∵∠2 =∠DBC,∠1=∠2,?
∴∠BCD =∠DBC.∴BD =DC.?
因此AB+AC＜2BD成立.
练习册系列答案
相关题目
ABCD中，设
=a，
=b.
