Question

设x、y满足约束条件

x-y+2≥0 4x-y-4≤0 x≥0 y≥0

，若目标函数z=ax+by（a＞0，b＞0）的最大值为6，则log 3(

1

a

+

2

b

)的最小值为

1

．

Answer 1

分析：作出x、y满足约束条件

x-y+2≥0 4x-y-4≤0 x≥0 y≥0

的图象，由图象判断同最优解，令目标函数值为6，解出a，b的方程，再由基本不等式求出

1

a

+

2

b

的最小值，代入求解即可

解答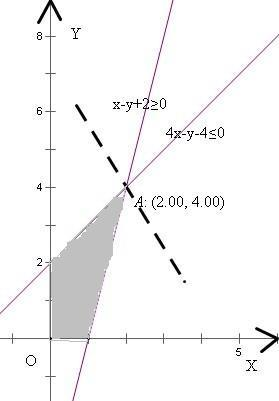：解：由题意、y满足约束条件

x-y+2≥0 4x-y-4≤0 x≥0 y≥0

的图象如图
目标函数z=ax+by（a＞0，b＞0）的最大值为6
从图象上知，最优解是（2，4）
故有2a+4b=6
∴

1

a

+

2

b

=

1

6

（2a+4b）(

1

a

+

2

b

)=

1

6

（10+

4b

a

+

4a

b

）≥

1

6

×（10+2

4b a × 4a b

）=3，等号当且仅当

4b

a

=

4a

b

时成立
故log 3(

1

a

+

2

b

)的最小值为log₃3=1
故答案为1

点评：本题考查简单线性规划的应用及不等式的应用，解决本题，关键是根据线性规划的知识判断出取最值时的位置，即最优解，由此得到参数的方程，再构造出积为定值的形式求出真数的最小值．