题目内容
已知直线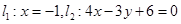 ,抛物线
,抛物线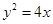 上有一动点P到直线
上有一动点P到直线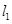 ,
, 的距离之和的最小值是( )
的距离之和的最小值是( )
A.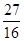 | B.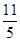 | C.3 | D.2 |
D
解析试题分析:设出抛物线上一点P的坐标,然后利用点到直线的距离公式分别求出P到直线l1和直线l2的距离d1和d2,求出d1+d2,利用二次函数求最值的方法即可求出距离之和的最小值.解:设抛物线上的一点P的坐标为(a2,2a),则P到直线l2:x=-1的距离d2=a2+1; P到直线l1:4x-3y+6=0的距离d1=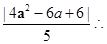 则d1+d2=
则d1+d2=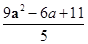 当a=
当a=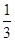 时,P到直线l1和直线l2的距离之和的最小值为2
时,P到直线l1和直线l2的距离之和的最小值为2
故答案为2
考点:抛物线的简单性质
点评:此题考查学生灵活运用抛物线的简单性质解决实际问题,灵活运用点到直线的距离公式化简求值,是一道中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知点 在直线
在直线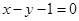 上运动,则
上运动,则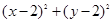 的最小值为( )
的最小值为( )
A.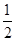 | B.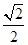 | C.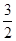 | D.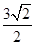 |
直线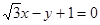 的倾斜角是( )
的倾斜角是( )
| A.30° | B.60° | C.120° | D.150° |
若直线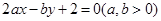 始终平分圆
始终平分圆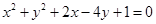 的周长,则
的周长,则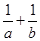 的最小值为( ).
的最小值为( ).
A.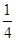 | B. | C. | D.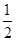 |
直线x+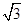 y-1=0的倾斜角是( )
y-1=0的倾斜角是( )
| A.150º | B.135º | C.120º | D.30º |
已知两条直线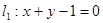 ,
,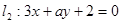 且
且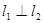 ,则
,则 =
=
A.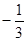 | B.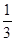 | C.-3 | D.3 |
过点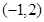 且与直线
且与直线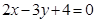 垂直的直线方程为
垂直的直线方程为
A.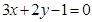 | B.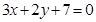 | C. | D.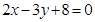 |
已知点A(-1,0);B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是
| A.(0,1) | B.(1-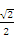 , , ) ( ) ( | C.(1-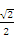 , ,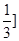 | D.[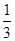 , , ) ) |
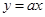 与
与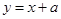 正确的是( )
正确的是( )