题目内容
(本小题满分14分)
已知函数
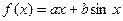 ,当
,当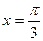 时,
时,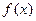 取得极
取得极 小值
小值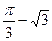 .
.(1)求
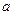 ,
,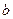 的值;
的值;(2)设直线
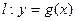 ,曲线
,曲线 .若直线
.若直线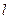
 与曲线
与曲线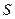 同时满足下列两个条件:
同时满足下列两个条件:①直线
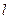 与曲线
与曲线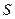 相切且至少有两个
相切且至少有两个 切点;
切点; ②对任意
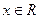 都有
都有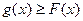 .则称直线
.则称直线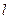 为曲线
为曲线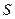 的“上夹线”.
的“上夹线”.试证明:直线
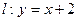 是曲线
是曲线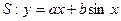 的“上夹线”.
的“上夹线”.(3)记
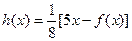 ,设
,设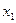 是方程
是方程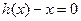 的实数
的实数 根,若对于
根,若对于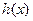 定义域中任意的
定义域中任意的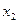 、
、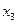 ,当
,当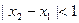 ,且
,且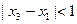 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数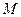 ,使得
,使得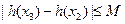 恒成立,若存在请求出
恒成立,若存在请求出 的值;若不存在请说明理由.
的值;若不存在请说明理由.(1)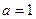 ,
,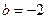 …………………………………………3分
…………………………………………3分
(2)由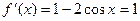 ,得
,得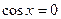 ,当
,当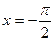 时,
时,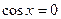 此时
此时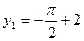 ,
,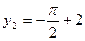 ,
,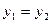
 所以
所以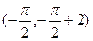 是直线
是直线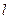 与曲线
与曲线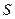 的一个切点,
的一个切点,
当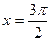 时,
时,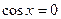 ,
,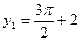 ,
,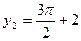 ,
,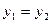
所以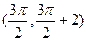 是直线
是直线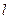 与曲线
与曲线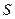 的一个切点
的一个切点
所以直线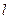 与曲线
与曲线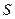 相切且至少有两个切点……6分
相切且至少有两个切点……6分
对任意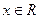 ,
,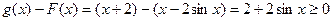
所以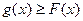 ,因此直线
,因此直线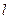 :
: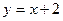 是曲线
是曲线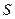 :
: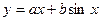 的“上夹线” …9分
的“上夹线” …9分
(3)方法一: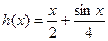 ,
,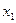 为
为 的根,即
的根,即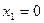 ,也即
,也即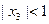 ,
,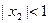 ………10分
………10分
而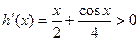
∴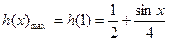 ,
,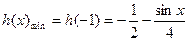
∴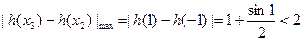 ……………………………13分
……………………………13分
所以存在这样最小正整数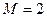 使得
使得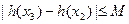 恒成立.………14分
恒成立.………14分
方法二:不妨设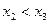 ,因为
,因为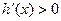 ,所以
,所以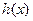 为增函数,所以
为增函数,所以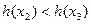
又因为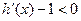 ,所以
,所以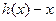 为减函数,所以
为减函数,所以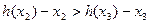
所以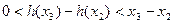 ,……………………11分
,……………………11分
即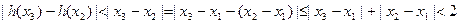 ………13分
………13分
故存在最小正整数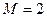 ,使得
,使得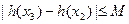 恒成立…………………14分
恒成立…………………14分
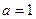 ,
,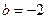 …………………………………………3分
…………………………………………3分(2)由
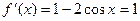 ,得
,得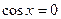 ,当
,当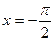 时,
时,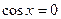 此时
此时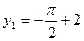 ,
,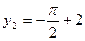 ,
,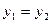
 所以
所以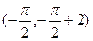 是直线
是直线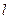 与曲线
与曲线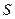 的一个切点,
的一个切点,当
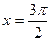 时,
时,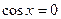 ,
,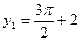 ,
,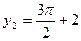 ,
,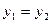
所以
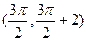 是直线
是直线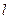 与曲线
与曲线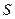 的一个切点
的一个切点 所以直线
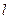 与曲线
与曲线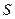 相切且至少有两个切点……6分
相切且至少有两个切点……6分对任意
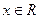 ,
,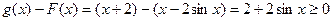
所以
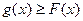 ,因此直线
,因此直线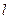 :
: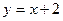 是曲线
是曲线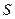 :
: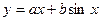 的“上夹线” …9分
的“上夹线” …9分(3)方法一:
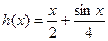 ,
,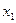 为
为 的根,即
的根,即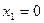 ,也即
,也即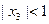 ,
,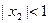 ………10分
………10分而
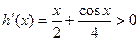
∴
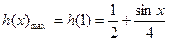 ,
,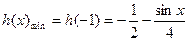
∴
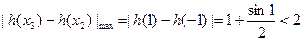 ……………………………13分
……………………………13分所以存在这样最小正整数
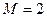 使得
使得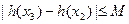 恒成立.………14分
恒成立.………14分方法二:不妨设
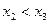 ,因为
,因为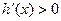 ,所以
,所以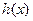 为增函数,所以
为增函数,所以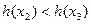
又因为
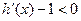 ,所以
,所以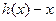 为减函数,所以
为减函数,所以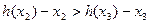
所以
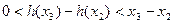 ,……………………11分
,……………………11分即
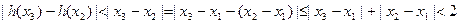 ………13分
………13分故存在最小正整数
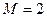 ,使得
,使得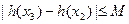 恒成立…………………14分
恒成立…………………14分略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

 所有正确结论的编号).
所有正确结论的编号).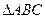 中,
中,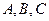 三内角所对的边分别为
三内角所对的边分别为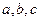 .
.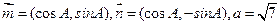 ,
,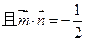
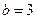 ,求
,求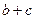 的最大值.
的最大值.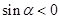 且
且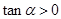 是,则
是,则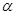 是( )
是( )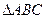 中,已知内角A、B、C成等差数列,边AC
中,已知内角A、B、C成等差数列,边AC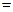 6。设内角
6。设内角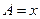 ,
,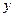 。
。
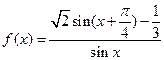 .
. 的定义域;
的定义域;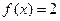 ,求
,求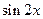 的值
的值 
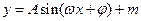 的最大值为4,最小值为0,最小正周期为2,直线
的最大值为4,最小值为0,最小正周期为2,直线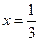 是其图像的一条对称轴,则下面各式中符合条件的解析式是( )
是其图像的一条对称轴,则下面各式中符合条件的解析式是( )



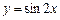 的图象按向量
的图象按向量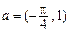 平移,所得图象的函数解析式是 .
平移,所得图象的函数解析式是 .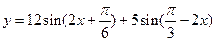 的最大值是( )
的最大值是( )