题目内容
 已知函数y=
已知函数y=| 1 | 2 |
(1)作出此函数在x∈[0,2π]的大致图象,并写出使y<0的x的取值范围;
(2)利用第(1)题结论,分别写出此函数在x∈R时,使y<0与y>0的x的取值范围.
分析:(1)由题意,可先列出表格,找出五点,再作出函数的图象,由图象写出使y<0的x的取值范围;
(2)由于此函数是一个周期是2π的周期函数,由所做的图象先找出函数在[0,2π]的上满足条件的区间,再由周期性同满足条件的所有区间即可
(2)由于此函数是一个周期是2π的周期函数,由所做的图象先找出函数在[0,2π]的上满足条件的区间,再由周期性同满足条件的所有区间即可
解答:解:(1)由题意,列出表格,
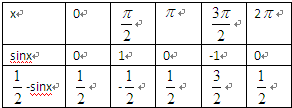
作出如图的图象

由图知,在x∈[0,2π]上,当x∈(
,
)时,y<0; (2分)
(2)由于函数y=
-sinx的周期是2π,由(1)知,
当x∈(2kπ+
,2kπ+
)时,y<0(2分)
当x∈(2kπ,2kπ+
)∪(2kπ+
,2kπ+2π)(k∈Z)时,y>0(2分)
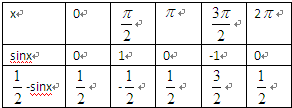
作出如图的图象

由图知,在x∈[0,2π]上,当x∈(
| π |
| 6 |
| 5π |
| 6 |
(2)由于函数y=
| 1 |
| 2 |
当x∈(2kπ+
| π |
| 6 |
| 5π |
| 6 |
当x∈(2kπ,2kπ+
| π |
| 6 |
| 5π |
| 6 |
点评:本题考点是正弦函数的图象,考查了正弦函数图象的作法-五点法及由函数的图象解三角不等式,解题的关键是由五点法作出函数的图象,及由图象解三角不等式,本题考查了作图与识图的能力,数形结合的思想

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目