题目内容
对于任意两个正整数,定义某种运算m、n;当m、n都为正偶数或正奇数时,mΔn=m+n;当m、n中一个为正奇数,另一个为正偶数时,mΔn=mn.则在上述定义下,M={(x,y)|xΔy=36,x∈N*,y∈N*},集合M中元素的个数为A.40 B.48
C.39 D.41
解析:当m、n都为正偶数或正奇数时,36=1+35=2+34=3+33=…=17+19=18+18,共18个等式,能组成的实数对(x,y)为18×2-1=35对;
当m、n中一个为正奇数,另一个为正偶数时,36=1×36=3×12=4×9,能组成的实数对(x,y)为3×2=6对,所以集合中共有41个元素.故选D.
答案:D

练习册系列答案
相关题目
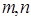 ,定义某种运算“※”如下:当
,定义某种运算“※”如下:当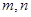 都为正偶数或正奇数时,
都为正偶数或正奇数时, 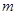 ※
※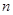 =
=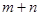 ;当
;当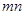 .则在此定义下,集合
.则在此定义下,集合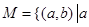 ※
※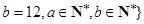 中的元素个数是( )
中的元素个数是( )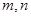 ,定义某种运算 “※”如下:当
,定义某种运算 “※”如下:当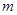 ※
※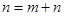 ;当
;当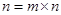 .则在此定义下,集合
.则在此定义下,集合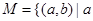 ※
※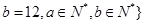 中的元素个数是 ( )
中的元素个数是 ( )