Question

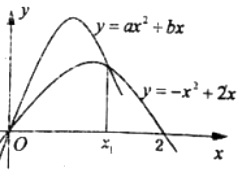
【题目】已知函数．

（Ⅰ）当时，求的单调区间；

（Ⅱ）设函数在点处的切线为，直线与轴相交于点.若点的纵坐标恒小于1，求实数的取值范围．

Answer 1

【答案】（Ⅰ）的单调递减区间为，单调递增区间为（Ⅱ）

【解析】试题分析：（Ⅰ）先明确函数定义域，再求函数导数，根据导函数零点进行分类讨论：当时， ，因此减区间为，当时， 递增区间为，递减区间为（Ⅱ）根据导数几何意义得切线的斜率，再根据点斜式写出切线方程，得点的纵坐标，即不等式恒成立，而不等式恒成立问题，一般转化为对应函数最值问题：： 的最大值，利用导数研究函数单调性，为单调递减，再利用洛必达法则得，因此，也可直接构造差函数，分类讨论最值进行求解

试题解析：解：（1）当时， .……………………1分

所以，当时， ；当时， .………………3分

所以函数的单调递减区间为，单调递增区间为.……………………4分

（2）因为，所以处切线的斜率，

所以切线的方程为，

令得， .………………………………5分

当时，要使得点的纵坐标恒小于1，

只需，即.…………………………6分

令，则.………………………………7分

因为，所以，

①若，即时， ，

所以，当时， ，即在上单调递增，

所以恒成立，所以满足题意.………………………………8分

②若即时， ，

所以，当时， ，即在上单调递减，

所以，所以不满足题意.…………………………9分

③若，即时， ，

则、、的关系如下表：

		0
	递减	极小值	递增

所以，所以不满足题意，

结合①②③，可得，当时， 时，此时点的纵坐标恒小于1.………………12分