题目内容
已知圆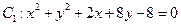 ,圆
,圆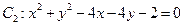 ,
,
试判断圆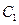 与圆
与圆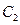 的关系。
的关系。
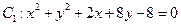 ,圆
,圆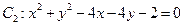 ,
,试判断圆
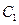 与圆
与圆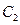 的关系。
的关系。相交
圆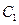 与圆
与圆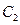 的方程联立,得到方程组
的方程联立,得到方程组
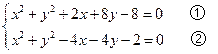
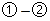 ,得
,得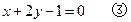 ,
,
由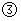 ,得
,得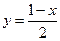 ,
,
把上式代入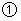 ,并整理,得
,并整理,得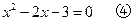
方程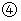 根的判别式
根的判别式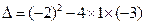
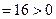 ,
,
所以,方程 有两个不相等的实数根
有两个不相等的实数根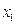 ,
,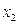 ,把
,把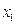 ,
,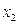 分别代入方程
分别代入方程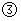 ,
,
得到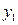 ,
,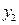 .
.
因此圆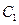 与圆
与圆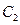 有两个不同的公共点
有两个不同的公共点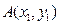 ,
,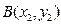 .
.
解法二:把圆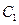 的方程化成标准方程,
的方程化成标准方程,
得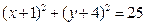 .
.
圆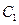 的圆心是点
的圆心是点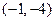 ,半径长
,半径长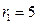 .
.
把圆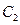 的方程化成标准方程,得
的方程化成标准方程,得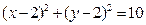 ,
,
圆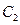 的圆心是点
的圆心是点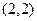 ,半径长
,半径长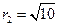 .
.
圆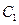 与圆
与圆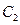 的连心线的长为
的连心线的长为
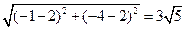 ,
,
圆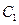 与圆
与圆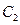 的两半径之和是
的两半径之和是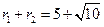 ,两半径长之差
,两半径长之差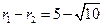 .
.
而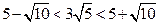 ,即
,即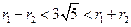 ,所以圆
,所以圆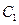 与圆
与圆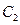 相交,它们有两个公共点
相交,它们有两个公共点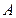 ,
,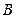
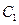 与圆
与圆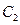 的方程联立,得到方程组
的方程联立,得到方程组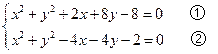
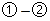 ,得
,得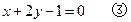 ,
,由
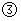 ,得
,得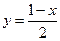 ,
,把上式代入
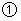 ,并整理,得
,并整理,得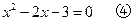
方程
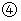 根的判别式
根的判别式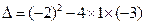
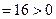 ,
,所以,方程
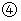 有两个不相等的实数根
有两个不相等的实数根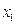 ,
,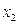 ,把
,把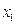 ,
,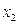 分别代入方程
分别代入方程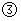 ,
,得到
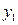 ,
,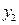 .
.因此圆
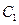 与圆
与圆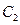 有两个不同的公共点
有两个不同的公共点 ,
, .
.解法二:把圆
 的方程化成标准方程,
的方程化成标准方程,得
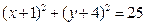 .
.圆
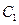 的圆心是点
的圆心是点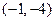 ,半径长
,半径长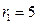 .
.把圆
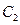 的方程化成标准方程,得
的方程化成标准方程,得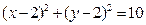 ,
,圆
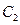 的圆心是点
的圆心是点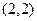 ,半径长
,半径长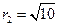 .
.圆
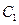 与圆
与圆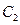 的连心线的长为
的连心线的长为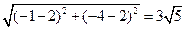 ,
,圆
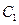 与圆
与圆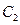 的两半径之和是
的两半径之和是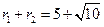 ,两半径长之差
,两半径长之差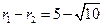 .
.而
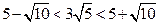 ,即
,即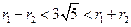 ,所以圆
,所以圆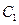 与圆
与圆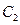 相交,它们有两个公共点
相交,它们有两个公共点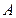 ,
,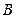

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
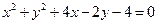 ,则
,则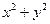 的最大值是 .
的最大值是 .
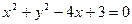 和
和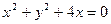 都外切,则动圆圆心的轨迹为( )
都外切,则动圆圆心的轨迹为( )